SA and SA IS
定义¶
字符串的下标从 \(1\) 开始。
定义 \(\operatorname{Suffix}(s,i)\) 表示的是 \(s\) 中 \([i,\operatorname{Len}(s)]\) 的这一段后缀。
后缀数组 \(\operatorname{SA}(s,i)\) 表示的是给出一个长度为 \(n\) 的字符串 \(s\),排名为 \(i\) 的后缀是 \(\operatorname{Suffix}(s,\operatorname{SA}(s,i))\),如果省略掉 \(i\),表示的是整个数组本身。显然这是一个排列,其逆排列记作 \(\operatorname{rank}(s,i)\),表示后缀 \(\operatorname{Suffix}(s,i)\) 的排名。 通常,我们只有一个串 \(s\),所以把 \(\operatorname{SA}(s,i)\) 简单记为 \(\operatorname{SA}(i)\)。
字符 \(\texttt{#}\) 是不会出现在原串里,且小于原串所有字符的字符。
SA-IS¶
下面简述 \(O(n)\) 求出 \(\operatorname{SA}\) 的方法。
为了方便起见,我们设字符串末尾,即第 \(n\) 个字符是 \(\texttt{#}\)。
L-type, S-type 与 LMS 后缀¶
若 \(\operatorname{Suffix}(s,i)<\operatorname{Suffix}(s,i+1)\),则它是一个 \(\text{S-type}\) 后缀,否则为 \(\text{L-type}\) 后缀。认为 \(\operatorname{Suffix}(n,i)\) 是 \(\text{S-type}\) 的。
称 \(\text{LMS}\) 后缀是每个 \(\text{S-type}\) 区间中最左侧的那一个,也就是 \(\operatorname{Suffix}(s,i)\) 为 \(\text{S-type}\) 且 \(\operatorname{Suffix}(s,i-1)\) 为 \(\text{L-type}\) 的 \(\operatorname{Suffix}(s,i)\)。
引理 1: 先考虑怎么求出每个后缀的类型,我们可以证明 \(\operatorname{Suffix}(s,i)\) 是 \(\text{S-type}\) 的,当且仅当:
- \(s_i<s_{i+1}\)
- \(s_i=s_{i+1}\land \operatorname{type}(i+1)=\text{S}\)
两个中有一个成立。 证明就是只要开头一直相同,就不断删掉开头字符后向后比较。归纳即可。
再考虑怎么利用后缀的类型进行排序。
引理 2: 若 \(\operatorname{Suffix}(s,i)\) 是 \(\text{S-type}\) 的而 \(\operatorname{Suffix}(s,j)\) 是 \(\text{L-type}\) 的,且 \(s_i=s_j\),那么 \(\operatorname{Suffix}(s,i)>\operatorname{Suffix}(s,j)\)。
不妨假设 \(\operatorname{Suffix}(s,i)=abX\),\(\operatorname{Suffix}(s,j)=acY\),且 \(a\neq b,a\neq c\),那么 \(c<a<b\),从而 \(\operatorname{Suffix}(s,i)>\operatorname{Suffix}(s,j)\)。
如果单侧取到等号,结果不会改变。两侧都取等,那么消掉第一个,继续向后递归,由引理 \(1\) 可以证明,后缀类型不改变。
LMS 子串¶
我们称两个相邻的 \(\text{LMS}\) 后缀的开头之间的一个部分,含这两个 \(\text{LMS}\) 后缀的开头,是一个 \(\text{LMS}\) 子串。
所有非 \(\texttt{#}\) 的 \(\text{LMS}\) 子串长度一定 \(>2\),因为在两个 \(\text{S-type}\) 之间一定要有一个 \(\text{L-type}\)。
从而可以证明 \(\text{LMS}\) 子串的个数不超过 \(\left\lceil\dfrac{|s|}{2}\right\rceil\) 个。
引理 3: 对任意两个 LMS 子串,不存在一个 LMS 子串是另外一个 LMS 子串的真前缀。
假设 \(A\) 是 \(B\) 的真前缀,那么 \(B\) 中一定至少有开头,末尾,\(A\) 末尾,三个位置是某一个 \(\text{LMS}\) 后缀的开头,不符合定义。
不难发现所有 \(\text{LMS}\) 子串长度和 \(<2|s|\),所以如果存在一个方法线性把他们排序,再把每个 \(\text{LMS}\) 子串压缩,变成它的排名,那么就只有 \(\left\lceil \dfrac{|s|}{2}\right\rceil\) 个字符,称压缩成的新字符串是 \(s'\)。
引理 4: \(s'\) 中每个后缀的排名就等于是 \(s\) 中每个 \(\text{LMS}\) 后缀(这里不是子串)的排名。
没有两个 \(\text{LMS}\) 子串,一个是另一个的真前缀,所以被比较的要么完全相同,要么至少一个位置字符不同,或类型不同。 前两种情况比较能看的出来后缀的大小,对于最后一种情况(类型不同),考虑引理 1,也能比较出对应后缀的大小。
诱导¶
如果我们能 \(O(n)\) 把从 \(\operatorname {SA}(s')\) 的后缀排序结果诱导出 \(\operatorname{SA}(s)\) 的后缀排序结果,那么我们不断递归,每次折半,算出下一半的部分后再诱导出当前的结果,总复杂度是
也就是 \(O(n)\) 的。那么我们先考虑,如果我们已经给出了这个 \(\text{LMS}\) 子串压缩后的字符串的 \(\text{SA}\),怎么求出原串的 \(\operatorname{SA}\) 数组。
接下来的部分对着代码讲,先给出代码:
// lms[i] 是将所有 LMS 子串排序后,排名为 i 的 LMS 子串的起始位置
void induce (int n, int m, std::vector<int> &a, std::vector<int> &lms, std::vector<int> &type) {
auto pushBack = [=](const int &x) {SA[tmp[a[x]]--] = x;};
auto pushFront = [=](const int &x) {SA[tmp[a[x]]++] = x;};
memset(cnt, 0, (n + 1) * sizeof(int));
memset(SA , -1, (n + 1) * sizeof(int));
for (int i = 1; i <= n; i++) cnt[a[i]]++;
for (int i = 1; i <= n; i++) cnt[i] += cnt[i - 1];
for (int i = 1; i <= n; i++) tmp[i] = cnt[i];
for (int i = m; i >= 1; i--) pushBack(lms[i]);
/* L-type 部分 */
for (int i = 1; i <= n; i++) tmp[i] = cnt[i - 1] + 1;
for (int i = 1; i <= n; i++)
if (SA[i] > 1 && type[SA[i] - 1] == 0)
pushFront(SA[i] - 1);
/* S-type 部分 */
for (int i = 1; i <= n; i++) tmp[i] = cnt[i];
// 把所有 S-type Suffix 全部重置
for (int i = n; i >= 1; i--)
if (SA[i] > 1 && type[SA[i] - 1] == 1)
pushBack(SA[i] - 1);
}
由引理 2,我们知道对于任意一对首字母相同,类型不同的后缀,\(\text{L-type}\) 的总是小于 \(\text{S-type}\) 的。
考虑 \(\text{SA}\) 里首字母为 \(c\) 的这段区间,前半部分是 \(\text{L-type}\) 后缀,后半部分是 \(\text{S-type}\) 后缀。
pushFront 和 pushBack 两个函数分别是从尾和从头插入桶(箭头指的是往哪边插入),type[i] 为 \(0\) 说明这是 \(\text{L-type}\),否则是 \(\text{S-type}\)。
\(11\sim 12\) 行,我们先对把所有 \(\operatorname{LMS}\) 后缀随便选择一个它所属的桶里的位置填进去。它们只要随便放在一个 \(\text{S-type}\) 部分的位置,并保证相对顺序即可,所以我们倒着枚举,逐个插到所属的 \(\text{S-type}\) 的末尾。
\(15\sim 18\) 行在填写 \(\text{L-type}\) 后缀的排名。现在所有 \(\operatorname{SA}(i)>0\) 的位置 \(i\) 都对应着一个 \(\text{LMS}\) 后缀了。并且 \(\operatorname{SA}(1)\) 必定是 \(\texttt{#}\) 所对应的 \(\text{LMS}\) 后缀(因为它最小)。每一个这样的 \(\text{LMS}\) 后缀,原串里对应的前面的位置都应当是一整串 \(\text{L-type}\) 后缀,并且这段 \(\text{L-type}\) 的首字母都比这个 \(\text{LMS}\) 后缀的首字母大(可以由引理 1 推出),也就是对应的排名比这个 \(\text{LMS}\) 大,位于 \(\text{SA}\) 的更后面的位置。
那么,\(\operatorname{SA}(i)-1\) 就是这一串 \(\text{L}\) 的末尾,也是这一段 \(\text{L-type}\) 后缀中的最小值。
我们把这个东西填入到当前的 \(\text{SA}\) 里,填写的就是最靠前的那个位置:
当我们的指针从前往后,扫到这个已经填了的位置 \(k\) 之后,\(\text{SA}(k)\) 指向它位于的这个红色的位置。
这个时候 \(\text{SA}(k)-1\) 就是蓝色这个位置,同样是 \(\text{L-type}\),那他在 \(\text{SA}\) 里的位置(即排名)就应该恰好位于 - 后面。
指针继续向后扫,现在扫到第二个 -,那么 \(\text{SA}(cur)-1\) 就对应的是绿色的位置……以此类推,我们就能把一整段 \(\text{L}\) 全都定下来。
类似地,我们就可以定下所有 \(\text{S-type}\) 后缀的排名。
问题就是怎么 \(O(|s|)\) 给 \(\text{LMS}\) 子串排序了。给出一个结论:
引理 5: 只需要确定每个桶 \(\text{S-type}\) 桶的起始位置。将每一个 \(\text{LMS}\) 后缀的首字母(即 \(\text{LMS}\) 字符)按照任意顺序放入对应的桶中,随后直接执行诱导排序即可。 证明懒得证了参考 这篇博客
给出完整代码:
// SA[i] -> 排名为 i 的后缀的起始点
// 注意这些数组是全局的
int SA[N], rk[N], cnt[N], tmp[N];
void induce (int n, int m, std::vector<int> &a, std::vector<int> &lms, std::vector<int> &type) {
auto pushBack = [=](const int &x) {SA[tmp[a[x]]--] = x;};
auto pushFront = [=](const int &x) {SA[tmp[a[x]]++] = x;};
memset(cnt, 0, (n + 1) * sizeof(int));
memset(SA , -1, (n + 1) * sizeof(int));
// 需要注意, 请务必保证字符集是 [1, n + 1], 否则这里会出错
// 比如长度为 1 的字符串 "z", 这里如果 "z" 直接按 ASCII 转过来会出错
// 最好不要 n 与字符集取 max, 手动离散化一下
for (int i = 1; i <= n; i++) cnt[a[i]]++;
for (int i = 1; i <= n; i++) cnt[i] += cnt[i - 1];
for (int i = 1; i <= n; i++) tmp[i] = cnt[i];
// 把 LMS 后缀按顺序插入
for (int i = m; i >= 1; i--) pushBack(lms[i]);
for (int i = 1; i <= n; i++) tmp[i] = cnt[i - 1] + 1;
for (int i = 1; i <= n; i++)
if (SA[i] > 1 && type[SA[i] - 1] == 0)
pushFront(SA[i] - 1);
for (int i = 1; i <= n; i++) tmp[i] = cnt[i];
// 把所有 S-type Suffix 全部重置
for (int i = n; i >= 1; i--)
if (SA[i] > 1 && type[SA[i] - 1] == 1)
pushBack(SA[i] - 1);
};
// a[0] 为空字符 c1, a[n + 1] 为空字符 c2 且 c1 < c2
// 从而 SA[1] 一定是 n + 1
inline void SAIS(int n, std::vector<int> &a) {
std::vector<int> type(n + 1, -1);
//递归到下一层的时候要多加一个空字符, 保险起见多开一个
std::vector<int> LMS(n + 2, 0);
type[n] = 1;
int m = 0;
// 先确定下类型
for (int i = n - 1; i >= 1; i--) {
if (a[i] == a[i + 1])
type[i] = type[i + 1];
else
type[i] = (a[i] < a[i + 1]);
}
// 这里的 rk 是后缀 i 的 LMS 编号
for (int i = 1; i <= n; i++) {
if (type[i] == 1 && type[i - 1] == 0) {
LMS[++m] = i;
rk[i] = m;
} else {
rk[i] = -1;
}
}
// LMS 子串现在是一个随便的顺序
induce(n, m, a, LMS, type);
// 现在所有 LMS 子串就排好序了
int tot = 0;
// 空字符, 防止 LMS[x + 1] 或者 LMS[y + 1] 不存在
LMS[m + 1] = n;
std::vector<int> nxt(m + 1, 0);
// nxt[i] 是 LMS[i] 在所有 LMS 子串中的排名
// 从小到大枚举所有 LMS 子串, 数有多少对相同的, 因为已经排好序, 数相邻的
// 考虑压缩后的那个字符串, 如果所有字符两两不同(没有一对相同的 LMS 子串)
// 那 LMS 后缀排名显然和 LMS 子串的排名一样
for (int i = 1, x, y; i <= n; i++) {
x = rk[SA[i]];
if (x == -1)
continue;
// 长度不同,可以直接判断不同
if (tot == 0 || LMS[x + 1] - LMS[x] != LMS[y + 1] - LMS[y])
tot++;
else
// 一个个字符比较, 如果不同就是不同
for (int p1 = LMS[x], p2 = LMS[y]; p2 <= LMS[y + 1]; p1++, p2++)
if (a[p1] != a[p2] || type[p1] != type[p2]) {
tot++;
break;
}
// 第 x 个 LMS 子串排名为 tot
nxt[x] = tot;
y = x;
}
// 如果所有 LMS 子串两两不同
if (tot == m)
// SA[排名] = 原串位置
for (int i = 1; i <= m; i++)
SA[nxt[i]] = i;
else
// 递归对这个字符串再后缀排序一次
SAIS(m, nxt);
// 此处 SA[i]: 排名为 i 的 LMS 后缀在原数组中的位置
// 把 nxt 变成排好序的 LMS 子串序列
for (int i = 1; i <= m; i++)
nxt[i] = LMS[SA[i]];
induce(n, m, a, nxt, type);
}
Height¶
存在性命题魅力时刻。
下面记 \(\operatorname{suf}(i)=\operatorname{Suffix}(s,i)\),略去 \(\operatorname{rank}(s,i)\) 中的 \(s\),简记 \(\operatorname{LCP}(\operatorname{suf}(i),\operatorname{suf}(j))\) 为 \(\operatorname{LCP}(i,j)\),定义:
定义 \(\operatorname{height}(1)=0\)。 一个简单的引理:
引理 6: 若 \(\operatorname{rank}(i)<\operatorname{rank}(j)<\operatorname{rank}(k)\),则:
\[ \left|\operatorname{LCP}(i,j)\right|,\left|\operatorname{LCP}(j,k)\right|\ge \left|\operatorname{LCP}(i,k)\right| \]
考虑 \(\operatorname{height}\) 具有什么性质,根据通用的增量的思想,不妨假设已经算出了 \(\operatorname{height}(i)\),并且它 \(>0\),那么容易算出各去掉第一个字符后的 \(\operatorname{LCP}\),即 \(\left|\operatorname{LCP}\left(\operatorname{SA}(i)+1,\operatorname{SA}(i-1)+1\right)\right|\),且:
记 \(p=\operatorname{SA}(i)+1,q=\operatorname{SA}(i-1)+1\)。
他们的第一个字符相同(\(\operatorname{LCP}>0\)),所以:
联想到上面的引理 \(6\),既然 \(p,q\) 的 \(\operatorname{LCP}\) 是 \(\operatorname{height}(i)-1\),那往他们中间插入一个 \(r\) 来凑成引理 \(6\) 的形式。
\(\operatorname{rank}(p),\operatorname{rank}(q)\) 是它们在 \(\operatorname{SA}\) 数组里的下标,但他们很可能不相邻,我们取 \(r\) 满足 \(\operatorname{rank}(r)=\operatorname{rank}(p)-1\),此时 \(r,p\) 对应的后缀在 \(\operatorname{SA}\) 里就是相邻的了,从而 \(\operatorname{height}(\rank(p))=\operatorname{LCP}(r,p)\),那么:
那么根据引理 \(6\),有:
这也就是
因为 \(p=\operatorname{SA}(i)+1\),所以有一般性的结论
至多 \(O(n)\) 次减法,那么暴力就能线性了。
// 枚举一个串的起始点
for(int i = 1, k = 0; i <= n; i++) {
if (k) k--;
/* 需要保证 s[0] 和 s[n] 是空字符 */
while (s[i + k] == s[SA[rk[i] - 1] + k]) k++;
ht[rk[i]] = k;
}
应用¶
Example 1: 求出字符串 \(\operatorname{suf}(i)\) 与 \(\operatorname{suf}(j)\) 的最长公共前缀
根据结论 \(1\),\(\left|\operatorname{LCP}(\operatorname{rank}(i),\operatorname{rank}(j))\right|\le \left|\operatorname{LCP}(\operatorname{rank}(k),\operatorname{rank}(k-1))\right|\),其中 \(k\in (i,j]\),而它们全部 \(\operatorname{LCP}\) 起来,可以得到 \(\operatorname{LCP}(i,j)\),也就是说,这个等号可以被取到,即:
问题就是 \(\text{RMQ}\) 了。
给个 \(\operatorname{height}\) 之所以被称为 \(\operatorname{height}\) 的原因图:
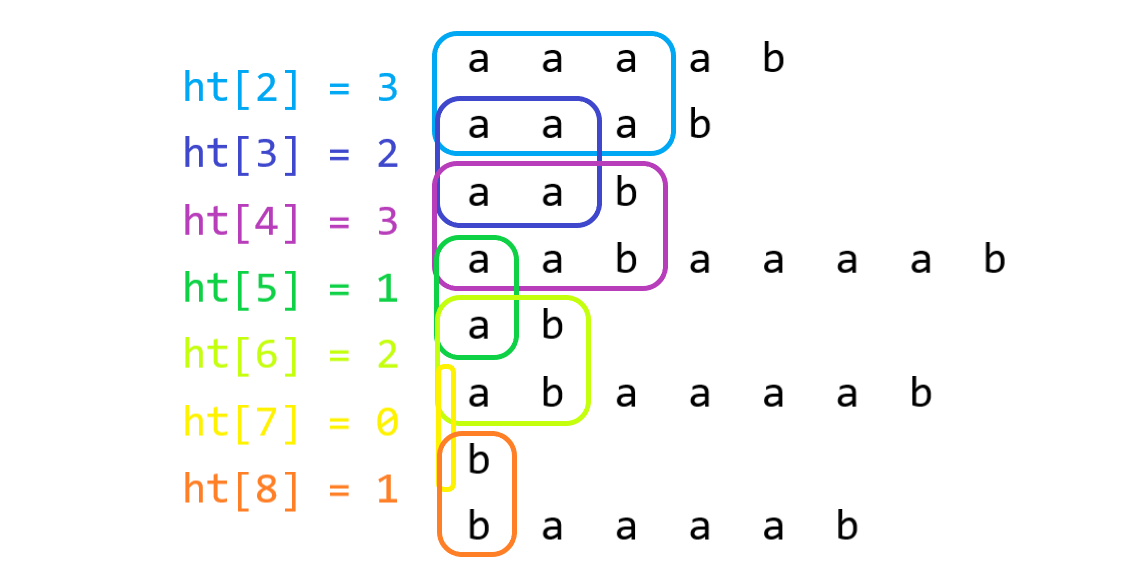
Example 2: 给出一个字符串,求本质不同子串数。
设 \(S\) 是已经加入的后缀的集合,那么加入一个新的后缀 \(i\) 的贡献是:
为了使用引理 7,从小到大枚举 \(i\),加入后缀 \(\operatorname{suf}(\operatorname{SA}(i))\),那么使得与它 \(\operatorname{LCP}\) 最长的就是 \(\operatorname{suf}(\operatorname{SA}(i-1))\),从而答案为:
小结¶
\(\operatorname{SA}\) 和 \(\operatorname{rank}\) 提供的是在排名与原串之间相互切换的方式。
- 如果一个跟字符串自身相关的东西是可以增量维护的,那么考虑在原串上做。