EX 2.2 后缀数据结构练习题
切り開け Star Divine
譲れない未来へ
負けないで Star Divine
未来を見捨てないで
立ち上がれ Star Divine
何度傷ついても
舞台に生かされている
切っ先に栄光止まれ
除了一些比较重要的 Trick,基本是 SAM 和 SA 随机选择一个做的。
参考资料:
基础内容¶
P2408 不同子串个数¶
SA¶
建出 \(\SA\) 和 \(\height\),在 \(\SA\) 上扫一遍,考虑 \(\SA(i)\) 和 \(\SA(i-1)\) 的重合情况,只有 \(\height(i)\) 个子串是重复的,加上 \(n-\SA(i)+1-\height(i)\) 即可。
SAM¶
显然这是 SAM 的 DAG 上从根节点出发的路径数。也是 Link 树的 \(\displaystyle\sum_{u}\len(u)-\len(\fa (u))\)。
P2178 [NOI2015] 品酒大会¶
SA¶
我们倒序求出所有答案,按 \(\height\) 从大到小扫描,假设当前的为 \(k\),那么只保留所有 \(\height(i)=k\) 的所有位置 \(i\),令这些位置的 \(\SA(i)\) 与 \(\SA(i-1)\) 连边。每个连通块中两个点 \(p,q\) 一定都是 \(k\) 相似的。用并查集维护即可,对每个连通块维护最大,最小,次大,次小,剩下的都是容易的。
SAM¶
首先建出后缀树。在后缀树上 DFS,对于每个节点 \(u\),\(u\) 子树内的所有后缀一定至多是 \(\len(u)\) 相似的。
我们只需要对 \([\len(fa_u)+1,\len(u)]\) 这个区间更新答案,剩下的会在上面更新。更新实际上就是区间 \(\chkmax\) 和区间加 \(\dfrac{\siz(u)(\siz(u)-1)}{2}\)。线段树维护即可。
P4070 [SDOI2016] 生成魔咒¶
SAM 做法是平凡的,我们来讨论 SA 的做法。
尝试照搬 P2408 的做法,从前往后加入字符,答案是 \(\displaystyle\sum_{i=1}^n\displaystyle n-\SA(i)+1-\height(i)\)。
我们的做法是尝试在原来的序列上按 \(1\sim n\) 扫一遍,每次把 \(\SA\) 上的 \(\rank(i)\) 设置为可用的,然后计算 \(\rank(i)\) 的前驱和后继的贡献。
这个做法看起来没什么问题,但是随着字符串不断向后添加字符,有些位置的 \(\height\) 也会发生变化。
考虑从后往前添加字符,这样每个位置被添加进来时,后缀的所有字符也被添加进来了,\(\height\) 就不会发生变化。
我们把原串 \(S\) 翻转,从 \(n\rightarrow 1\) 逐个添加字符,计算 \(\rank(i)\) 和前驱后继的贡献即可。
P5341 [TJOI2019] 甲苯先生和大中锋的字符串¶
后缀树做法同样是简单的。
SA¶
讨论 \(k\ge 2\) 的情况。
如果一个子串恰好出现 \(k\) 次,那么这个子串的 \(\Startpos\) 集合在 \(\SA\) 上一定是一个长度为 \(k\) 的区间。
考虑枚举一个长度为 \(k\) 的区间,计算 \(\Startpos\) 集合恰好为这个区间的子串的贡献,设区间为 \([l,r]\),则所有 \(\Startpos\) 集合为这个区间,长度 \(L\) 满足: $$ \max(\height(l),\height(r+1))+1\le L\le \min_{l+1}^{r}{\height(i)} $$ 的子串都在序列中恰好出现了 \(k\) 次。
单调队列维护滑动窗口即可 \(\mathcal O(T(n+|\Sigma|))\)。
JZPGYZ - Sevenk Love Oimaster¶
SAM¶
首先建出模板串的广义 SAM,对于每个询问串,在广义 SAM 上沿着转移边转移,所到的节点代表的 \(\Endpos\) 集合就是这个子串出现位置的 \(\Endpos\) 集合。我们只需要数这些 \(\Endpos\) 来自多少个不同的串即可,即子树数颜色。
SA¶
首先用分割符把所有字符串串在一起,对整个串建 SA,对第 \(i\) 个询问串 \(t_i\),设其开头在整个串中的位置为 \(p_i\)。
该询问串为某个模板串的子串的条件是,与该模板串的某个后缀 \(\LCP\) 长度大于等于自身。
我们找到 \(\rank(p_i)\) 前后第一个 \(\height\) 小于 \(\len(t_i)\) 的,它们中所夹的这个区间就是与 \(t_i\) 的 \(\LCP\) 长度大于等于自身的后缀,我们只要数出这些后缀来自多少个不同的模板串即可,即区间数颜色。
P3975 [TJOI2015] 弦论¶
SA¶
来点纯正 \(\mathcal O(n)\) 做法!
首先 \(t=0\) 会做本质不同子串个数的都会。接下来讨论 \(t=1\) 怎么做。
根据本质不同子串个数的经验,\(\SA(i)\) 后缀中,长度 \(>\height(i)\) 的前缀才是新出现的子串。
从小到大扫描整个 \(\SA\),在每个子串第一次出现的时候统计贡献。
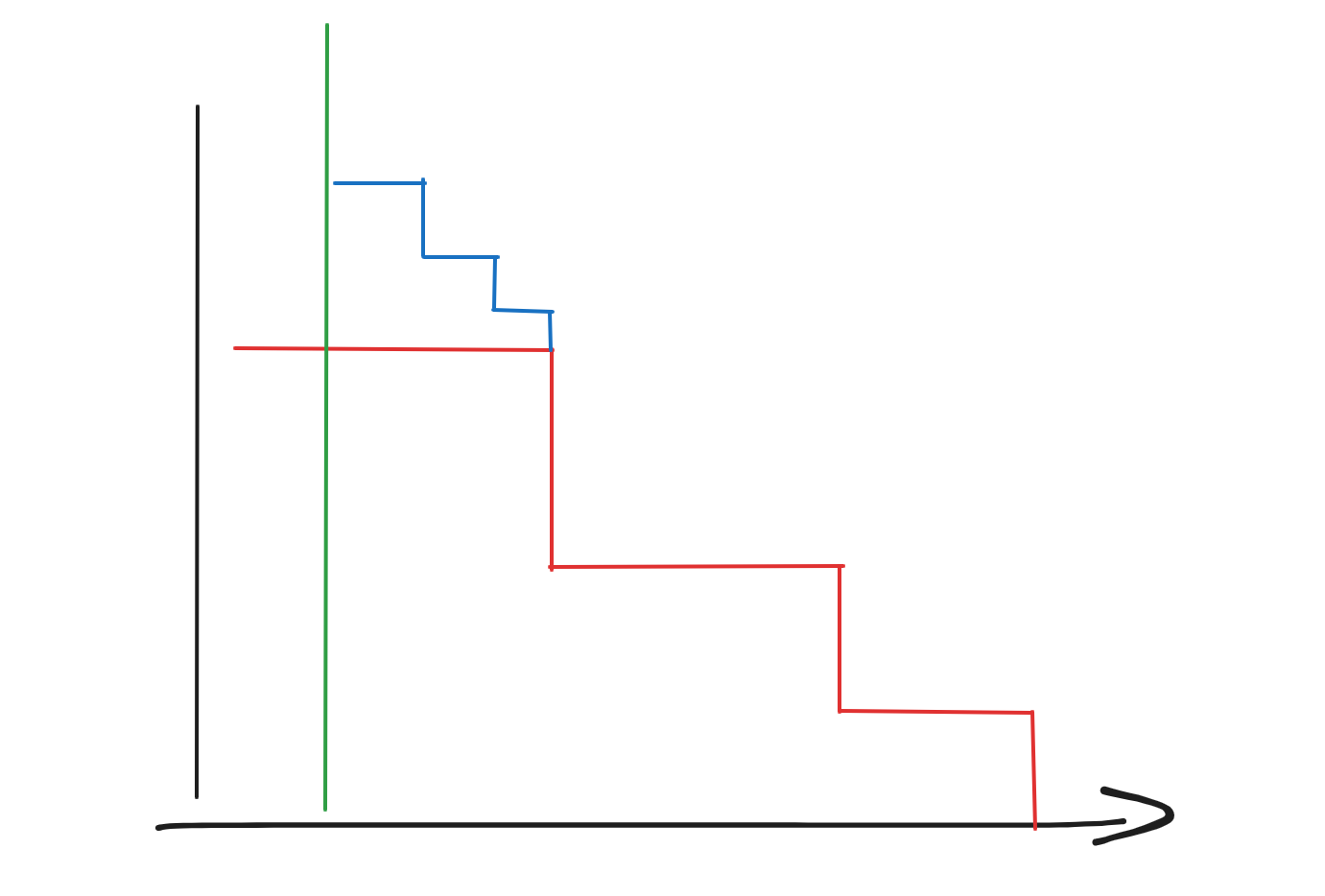
我们维护每个点向右 \(\height\) 的单调栈,把这些单调栈画出来:
比如黑线处的单调栈为红线这一条,向右移动到绿色的位置,有若干个原先被删掉的位置恢复了,红-蓝线夹着的这部分位置对应的子串就是之前没有被统计过的,也就是绿线代表的串长度 \(>\height\) 的部分。这部分的面积 \(p\) 就是新的子串个数。
如果 \(k\le p\),那么就说明所求的子串正是落在这一组新增的面积之中。枚举单调栈里的元素就能找出所求的子串。否则,令 \(k\leftarrow k-p\),在枚举的串中继续右移。
打不过 \(\mathcal O(n\log n)\),怄火。