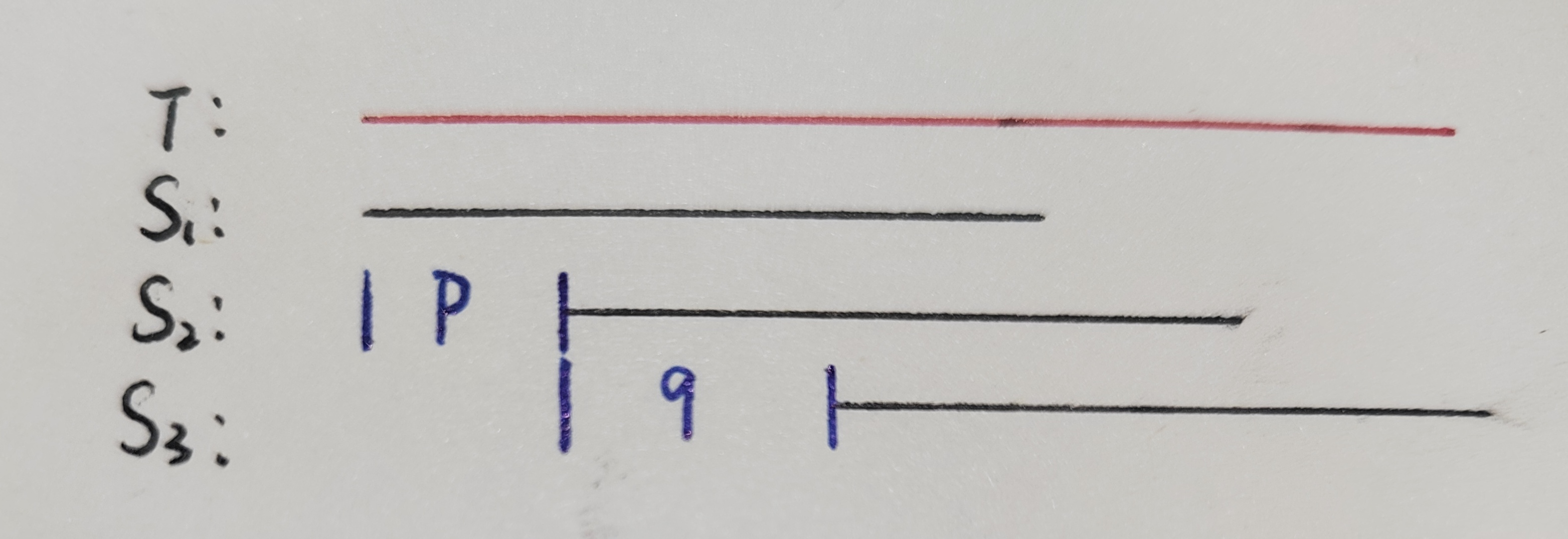2.1.2 Border论与回文

\[ \rm{Define\ \LaTeX \ Macros\ Here} \newcommand\stirA[2]{\begin{bmatrix}#1\\ #2\end{bmatrix}} \newcommand\stirB[2]{\begin{Bmatrix}#1\\ #2\end{Bmatrix}} \newcommand\ul[1]{\underline{#1}} \newcommand\dis{\operatorname{dis}} \newcommand\edp{\operatorname{edp}} \newcommand\Endpos{\operatorname{Endpos}} \newcommand\Startpos{\operatorname{Startpos}} \newcommand\height{\operatorname{height}} \newcommand\SA{\operatorname{SA}} \newcommand\len{\operatorname{len}} \newcommand\chkmax{\operatorname{chkmax}} \newcommand\chkmin{\operatorname{chkmin}} \newcommand\siz{\operatorname{siz}} \newcommand\fa{\operatorname{fa}} \newcommand\LCP{\operatorname{LCP}} \newcommand\EGF{\operatorname{EGF}} \newcommand\OGF{\operatorname{OGF}} \newcommand\bd{\operatorname{Border}} \newcommand\mbd{\operatorname{MaxBorder}} \]

KMP 的部分略。

\(\bd\) 的定义：我们称一个字符串 \(T\) 是字符串 \(S\) 的一个 \(\bd\)，当且仅当 \(T\) 既是 \(S\) 的前缀又是 \(S\) 的后缀。特别地，\(S\) 不是 \(S\) 的 \(\bd\)。

我们称字符串 \(S\) 的 \(\mbd\) 是串 \(S\) 所有 \(\bd\) 中最长的一个。

若有正整数 \(p\) 满足 \(\forall i\in [1,|S|-p],S[i]=S[i+p]\)，那么 \(p\) 则是 \(S\) 的一个周期。若 \(p\mid n\)，则 \(p\) 为 \(S\) 的一个整周期。

显然，\(p\) 为 \(S\) 的周期的充分必要条件是存在一个 \(S\) 的 \(\bd\) 为 \(T\)，满足 \(|S|-|T|=p\)。

显然，对字符串做 KMP，\(\text{Fail}\) 数组（或称 \(\text{Next}\) 数组）即为每个前缀的 \(\mbd\) 的长度。

下面设 \(\bd(S)\) 为 \(S\) 的 \(\bd\) 集合，\(\mbd(S)\) 为 \(S\) 的 \(\mbd\)。

Border 的一些性质¶

\(\bd(S)=\{\mbd(S)\}\cup \bd(\mbd(S))\)

即，\(\bd(S)\) 是 \(S\) 的 \(\mbd\) 再加上 \(\mbd\) 的 \(\bd\) 集合。

这个证明是平凡的，考虑比 \(\mbd\) 短的 \(\bd\) 是这样的
```
   Border: [----                  ----]
MaxBorder: [------              ------]
 String S: [--------------------------]
```
而前后缀相同，所以此 \(\bd\) 既是 \(\mbd\) 的前缀又是 \(\mbd\) 的后缀，所以 \(\mbd\) 也具有此 \(\bd\)。

所以 KMP 的过程中不断跳 \(\text{Fail}\)，到达的所有前缀组成的集合就是 \(\bd(S)\)。
强/弱周期引理

弱周期引理(Weak Periodicity Lemma, WPL):

若 \(p,q\) 为 \(S\) 的周期，且 \(p+q\le |S|\)，那么 \(\gcd(p,q)\) 同样为 \(S\) 的周期。

不妨钦定 \(p>q\)，设 \(d=p-q\)，那么：
1. 若 \(i>q\)，则 \(S[i]=S[i-q]=S[i-q+p]=S[i+d]\)。
2. 若 \(i<p\)，则 \(S[i]=S[i+p]=S[i+p-q]=S[i+d]\)。
显然这覆盖了所有的 \(i\)，那么 \(d\) 必然也是 \(S\) 的一个周期，如此辗转相减即有 \(\gcd(p,q)\) 为 \(S\) 的周期。

周期引理(Periodicity Lemma, PL):

若 \(p,q\) 为 \(S\) 的周期，且 \(p+q-\gcd(p,q)\le |S|\)，那么 \(\gcd(p,q)\) 同样为 \(S\) 的周期。

证明不会。

Border 与周期的等差数列性质¶

性质 1:

若 \(2|S|\ge |T|\)，那么 \(S\) 在 \(T\) 中的匹配位置(\(T\) 中 \(S\) 的所有起点)组成一个等差数列。若此等差数列有至少三项，则公差为 \(S\) 的最小周期。

首先将 \(T\) 前，后没有匹配 \(S\) 的部分去掉。

第一条线代表的是 \(S\) 的第一次匹配，第三条线是最后一次匹配，中间的线是第二次匹配。显然，\(p,q\) 都是 \(S\) 的周期。

由于 \(2|S|\ge |T|\)，我们有 \(|S|+p+q=|T|\)，那么就有 \(p+q=|T|-|S|\le |S|\)，根据 WPL，\(d=\gcd(p,q)\) 同样是 \(S\) 的周期。

我们不妨设 \(m\) 是 \(S\) 的最小周期，那么 \(m\le d\le p\le |S_1\cap S_2|\)，\(m\) 应当为 \(S_1\cup S_2\) 的周期。那么如果 \(m<p\)，将 \(S_1\) 右移 \(p\) 同样也会产生匹配，与 \(S_2\) 是第二次匹配矛盾。那么就必然有 \(p\) 是最小的周期。

所以 \(\gcd(p,q)=d=p\)，即 \(p\mid q\)。所以第一个间隔 \(p\) 就一定是 \(S\) 的最小周期。

不难发现以上推理没有用到 \(S_1\) 是第一个匹配的性质，如此即可推理得任何一个间隔都必定是 \(S\) 的最小周期。所以所有匹配位置一定组成一个等差数列。

性质 2:

一个字符串的所有 \(\bd\) 的长度构成 \(\mathcal O(\log n)\) 个等差数列。具体地，设 \(2^k\) 是 \(<|S|\) 的最大的 \(2\) 的幂，长度在区间 \([2^0,2^1)\) 内的 \(\bd\) 长度构成一个等差数列，\([2^1,2^2)\) 的构成另一个等差数列……最后长度在区间 \([2^k,|S|)\) 内的 \(\bd\) 构成一个等差数列。

为了证明此性质，我们先证明一个引理。

引理：

对于字符串 \(S\)，其长度 \(\ge \frac{|S|}{2}\) 的 \(\bd\) 长度构成一个等差数列。

我们只需要证明所有 \(\le \frac{|S|}{2}\) 的周期构成一个等差数列。

设字符串 \(S\) 的最短周期为 \(p\)，另有一周期 \(q\) 满足其是所有 \(\le \frac{|S|}{2}\) 的周期中最大的一个，那么 \(|S|-p,|S|-q\) 分别是某 \(\bd\) 的长度，根据 WPL，我们又有 \(\gcd(p,q)\) 是 \(S\) 的一个周期。因为 \(\gcd(p,q)\le p\)，而 \(p\) 又是最短周期，那必然就只能有 \(p\mid q\)。根据周期的定义，我们知道 \(p\) 是周期，\(2p\) 是周期，……，\((\frac{q}{p}-1)p\) 是周期，\(q\) 是周期，所以它们组成一个等差数列。

我们又能证明对于任意一个周期 \(q\le \frac{|S|}{2}\)，均满足 \(p\mid q\)，所以这就是所有长度小于等于 \(\frac{|S|}{2}\) 的周期。

接下来的证明就非常平凡了！

首先 \([2^k,n)\) 的部分我们已经完成了，因为 \(\frac{|S|}{2}\le 2^k\)。

那么接下来就是对任意一个 \(x<k\)，都有长度在 \([2^x,2^{x+1})\) 的 \(\bd\) 长度构成一个等差数列。

不妨设其中长度最大的 \(\bd\) 长度为 \(l\)，则所有原串中长度 \(<2^{x+1}\) 的 \(\bd\) 要么是这个最大的 \(\bd\)，要么是这个最大 \(\bd\) 的 \(\bd\)。

对这个长度为 \(l\) 的 \(\bd\) 施用引理，所有长度在 \([\frac{l}{2},l)\) 的 \(\bd\) 长度又构成一个等差数列，根据引理，长度的公差为最长 \(\bd\) 的周期，所以 \(l\) 可以放在这个等差数列的末尾。因为 \(\frac{l}{2}\le 2^x\)，所以长度在 \([2^x,2^{x+1}]\) 之间的 \(\bd\) 又构成一个等差数列。

还有一个性质：

性质 3:

对于字符串 \(S\)，其公差 \(\ge d\) 的 \(\bd\) 等差序列总长是 \(\mathcal O\qty(\frac{|S|}{d})\)。

证明不会。

应用¶

[WC2016] 论战捆竹竿¶

首先显然除了第一步必须延展 \(n\) 以外，其他都可以延展 \(S\) 的一个周期的长度，你可以延展任意多次，问 \([0,w-n]\) 里有哪些数是可以被凑出来的。

显然问题就是完全背包，因为 \(w\) 很大所以上个同余最短路。

复杂度是最小周期长度乘周期数量，显然是 \(\mathcal O(n^2)\)。

考虑怎么优化，显然所有周期构成 \(\mathcal O(\log n)\) 个等差数列。

显然考虑对每个等差数列单独处理，不妨设当前等差数列是 \(l_i,l_i+d_i,l_i+2d_i,\cdots, l_i+kd_i\)。我们在模 \(l_i\) 的意义下处理这个等差数列。

当然处理的方法不可能是把这里面每个东西都塞进去转移一遍。考虑令 \(x\rightarrow x+d_i\) 连边会形成 \(\gcd(l_i,d_i)\) 个环。不管用哪个 \(l_i+pd_i\) 转移，都不可能在两个环之间相互转移。

对每个环单独考虑，环里的最小值不会被任何一个其他点转移到。我们从最小值开始，转两圈。具体的说，我们从最小值开始（设其对应的是模 \(l_i\) 下的 \(s\)），断环成链，链上的每个位置 \(q\) 代表 \((s+qd)\bmod l_i\)，每个位置 \(x\) 可以被从 \(x-p\) 用 \(l_i+pd\) 的代价转移过来，此处 \(0\le p\le k\)。单调队列优化即可。

那么问题就是怎么从模 \(l_i\) 转移到模 \(l_j\) 了。设 \(f_{p,x}\) 模 \(p\) 意义下最小的，同余 \(x\) 的数，那么 \(f_{l_j,x}=\displaystyle\min_{f_{l_i,y}\bmod l_j=x}f_{l_i,y}\)。然后原先所有模 \(l_i\) 相同的都视为是同一个状态，所以还要再往同余最短路里加一个物品 \(l_i\)。