亚线性筛法初步¶
我们在本节中约定,符号 \(\operatorname{S}_f(n)\) 表示数论函数 \(f\) 的前 \(n\) 项和,即:
整除分块为我们揭示了整个序列仅仅只有 \(\mathcal O(\sqrt n)\) 个位置是非平凡的,那我们的前缀和为什么不能做到更好呢?
杜教筛¶
块筛¶
整除分块里,我们经常见到这样的式子
我们称 \(f\) 关于 \(n\) 的块筛是对于所有 \(k\) 满足 \(1\le k\le n\) 时,\(\operatorname{S}_f(\lfloor\frac{n}{k}\rfloor)\) 的值组成的集合。也就是整除分块的时候我们要的值。
整除的集合有着如下的性质:
-
性质 1: 设 \(R(n)=\{\lfloor\frac{n}{k}\rfloor: 1\le k\le n\}\),那么若 \(m\in R(n)\),则 \(R(m)\subseteq R(n)\)。
这是因为 \(\lfloor\frac{\lfloor\frac{n}{i}\rfloor}{j}\rfloor=\lfloor\frac{n}{ij}\rfloor\)。也就是,想要得到\(f\) 关于 \(n\) 的块筛,得到 \(kn\) 的即可。
-
性质 2: 设 \(\{r: \lfloor\frac{n}{r}\rfloor\neq \lfloor\frac{n}{r+1}\rfloor\}\),那么该集合即为 \(\{\lfloor\frac{n}{k}\rfloor: 1\le k\le n\}\)。
也就是整除分块的边界恰好是 \(\{\lfloor\frac{n}{k}\rfloor:1\le k\le n\}\),使用性质 1 即可证明。
杜教筛的两个形式¶
-
乘积式:
有数论函数(不必是积性) \(f,g,h\) 满足 \(h=f*g\),设我们已经知道了 \(f,g\) 的块筛结果,现在要求 \(h\) 的块筛结果。
\[ \begin{aligned} \operatorname{S}_h(n)&=\sum_{i=1}^{n}\sum_{d\mid i}f(d)g\qty(\frac{i}{d})\\ &=\sum_{d=1}^{n}f(d)\sum_{d\mid i,i\le n}^{}g\qty(\frac{i}{d})\\ &=\sum_{d=1}^{n}f(d)\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}g(i)\\ &=\sum_{d=1}^{n}f(d)\operatorname{S}_g\qty(\left\lfloor\frac{n}{d}\right\rfloor) \end{aligned} \]对每个 \(\lfloor\frac{n}{d}\rfloor\) 求一次就是类似二重整除分块的形式了,即复杂度是 \(\mathcal O(n^{3/4})\)。
如果 \(f,g\) 都是积性函数,那 \(h\) 也是积性函数。通过线性筛预处理前 \(\mathcal O(n^{2/3})\) 项的前缀和,可以把复杂度降低至 \(\mathcal O(n^{2/3})\)。
需要注意的一点是,\(f\) 并不一定需要非常容易计算前缀和,我们只需要它的块筛结果(前者显然隐含了后者)。因为我们对于某一项 \(\operatorname{S}_g(\lfloor\frac{n}{d}\rfloor)\),运用性质 2,所需要的 \(\operatorname{S}_f(d)\) 的 \(d\) 的值实际上有 \(d\in\{r: \lfloor\frac{n}{r}\rfloor\neq \lfloor\frac{n}{r+1}\rfloor\}\),也就是我们只需要它的块筛就够了。
-
除式:
有数论函数(不必是积性) \(f,g,h\) 满足 \(h=f*g\),设我们已经知道了 \(g\) 的块筛结果,\(h\) 是一个容易求单项前缀和的函数,现在要求 \(f\) 的块筛结果。
根据上面的推导我们已经知道
\[ \operatorname{S}_h(n)=\sum_{d=1}^{n}g(d)\operatorname{S}_f(\left\lfloor\frac{n}{d}\right\rfloor) \]我们要求 \(\operatorname{S}_f(n)\),所以单独把这一项拿出来
\[ \begin{aligned} \operatorname{S}_h(n)&=g(1)\operatorname{S}_f(n)+\sum_{d=2}^{n}g(d)\operatorname{S}_f(\left\lfloor\frac{n}{d}\right\rfloor)\\ g(1)\operatorname{S}_f(n)&=\operatorname{S}_h(n)-\sum_{d=2}^{n}g(d)\operatorname{S}_f(\left\lfloor\frac{n}{d}\right\rfloor) \end{aligned} \]运用性质 \(1\),我们记忆化这个过程,即可在 \(\mathcal O(n^{2/3})\) 的时间内求出 \(f\) 的块筛结果。
这两个形式的复杂度证明没有不同,都可以直接用 OI-wiki 上的这个推导。
总结一下,如果欲求 \(f\) 的块筛,可以试着构造一个易求块筛的函数 \(g\),使得 \(f/g\) 易求块筛,或 \(f*g\) 易求前缀和。
狄利克雷双曲线法¶
给出 \(f,g\) 的块筛,设 \(h=f*g\),求 \(\operatorname{S}_{h}(n)\)。
显然,我们知道
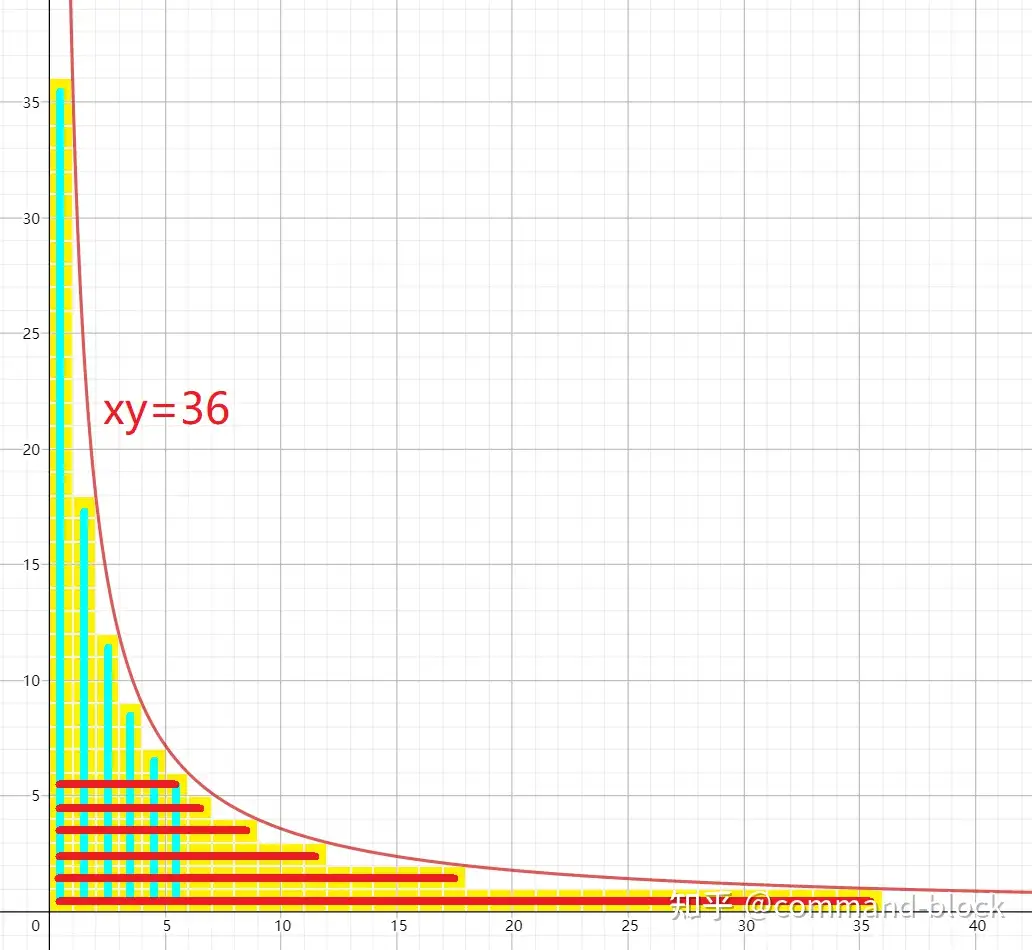
我们可以把这个东西写成
对于 \(x>\lfloor\sqrt n\rfloor\) 的情况,能贡献到 \(f(x)\) 的 \(g(y)\) 就肯定有 \(y\le \lfloor\sqrt n\rfloor\) 了。
那么我们的 \(f,g\) 都只枚举到前 \(\lfloor\sqrt n\rfloor\),就肯定能覆盖所有要求的位置的值了。
但是这样在两者都 \(\le \lfloor\sqrt n\rfloor\) 的时候就会算重,所以最终的式子就是
借助 Command_Block 知乎上的图
PN 筛¶
可以说是杜教筛(乘积式)的一个扩展。
Powerful Number¶
我们称一个正整数是一个 Powerful Number(PN),当且仅当其所有质因数的指数都 \(\ge 2\),特别的,\(1\) 是 PN。
引理 1:
所有 PN 均能被写成形如 \(a^2b^3\) 的形式。
证明:
对于每个 \(p^k\),如果 \(k\) 是偶数,那么把 \(p^{k/2}\) 放到 \(a\) 里,否则把 \(p\) 放到 \(b\) 里,\(p^{(k-3)/2}\) 放到 \(a\) 里。
或者更形式化地说:
$$ a=\prod p_i^{(k_i-3[k\bmod 2=1]) / 2}, b=\prod p_i^{[k_i\bmod 2 = 1]} $$
另外,这构成了一个 PN 到 \((a,b)\) 的单射(并不是所有 \((a,b)\) 都能对应一个 PN)。
这看起来说明 PN 的个数不会太多
定理 1:
PN 的个数为 \(\mathcal O(\sqrt n)\) 个。
证明:
放缩一下,计算数对 \((a,b)\) 的个数,这显然是 $$ \sum_{x=1}^{\sqrt n}\qty(\frac{n}{x^2})^{1/3} $$
我们转而计算积分 $$ \begin{aligned} &\phantom{=}\int_{1}^{\sqrt n}\qty(\frac{n}{x^2})^{1/3}\operatorname{d}x\ \end{aligned} $$
求不定积分
$$ \begin{aligned} &\phantom{=}\int\qty(\frac{n}{x^2})^{1/3}\operatorname{d}x\ &=\sqrt[3]n\int x^{-2/3}\operatorname{d}x\ &=\sqrt[3]n\cdot \frac{1}{\frac{1}{3}}\sqrt[3]x+C\ &=3\sqrt[3]n\sqrt[3]x+C \end{aligned} $$
定积分的结果显然是
$$ 3\sqrt n-3\sqrt[3]n $$
PN 筛¶
我们希望求出积性函数 \(f(n)\) 的块筛,PN 筛的想法是,构造一个积性函数 \(g\),满足在所有质数 \(p\) 处,有 \(g(p)=f(p)\),然后利用 PN 分析 \(h=f/g\) 的性质,最后利用 \(f=g*h\) 计算 \(f\)。
那么我们来试着分析一下 \(h=f/g\) 的性质。对于质数 \(p\),我们有: $$ f(p)=g(1)h(p)+g(p)h(1) $$ 那么由于 \(g(p)=f(p)\),显然只能有 \(h(p)=0\)。
考虑由于 \(h\) 是积性的,那么只能在 PN 处有值,其余位置都必为 \(0\)。 $$ \operatorname{S}f(n)=\sum\right\rfloor) $$ 这就有了一个 }(n)}h(i)\operatorname{S}_g\qty(\left\lfloor\frac{n}{i\(\mathcal O(n^{2/3})\) 的做法,但我们能做到 \(\mathcal O(n^{3/5})\)。
定理 2:
\(h\) 关于 \(n\) 的块筛只有 \(\mathcal O(n^{1/3})\) 个本质不同的值。
证明:
考虑 \(\operatorname{S}_h\qty(\left\lfloor\frac{n}{x}\right\rfloor)\),若 \(x\le \mathcal n^{1/3}\),那么显然就只有 \(\mathcal O(n^{1/3})\) 个值。
若 \(x> n^{1/3}\),那么 \(\left\lfloor\frac{n}{x}\right\rfloor\le n^{2/3}\),哪怕取遍 \(1\sim n^{2/3}\) 也只有 \(\mathcal O(\sqrt{n^{2/3}})=\mathcal O(n^{1/3})\) 个有值的 \(h\)。
那么处理单点的 $$ \operatorname{S}f(n)=\sum\right\rfloor) $$ 单次复杂度可以降至 }^{n}g(i)\operatorname{S}_h\qty(\left\lfloor\frac{n}{i\(\mathcal O(n^{1/3})\)。
类似杜教筛那样进行复杂度平衡,我们先线性筛至 \(t\)。 $$ \mathcal O\qty(t+\sum_{i=1}^{n/t}\qty(n/i)^{1/3}) $$ 取 \(t=n^{3/5}\),平衡得复杂度为 \(\mathcal O(n^{3/5})\)。