5.2.3 Top Cluster, Top Tree(上)

才能なんてないから

ここで一生泣いているんだろ

目に映った景色の青さが

羨ましく思っていた

参考资料

理论上的内容以上博客讲的已经非常好了，本文只做简要带过。

本文主要的内容将会是，Top Tree 具体怎么实现，以及如何用它解决各种题目。

感谢 llzer 给了我一份写的非常好的静态 Top Tree 实现参考！

Top Tree 基本理论¶

基本是复读。

边分树要引入大量的冗余信息，而且会对树的结构进行破坏，统计信息的时候还要注意新加的边与原来的边的区别。我们希望找到一个比它更好的二叉分治结构，可以不维护那么多冗余的信息。

引入簇(cluster)的概念：一个簇是树上的一个连通子图，满足簇内的点至多有两个与簇外的点有边相连。这两个点称为界点。簇路径指的是树上这两个界点之间的路径。

显然，初始每条树上的边都是一个簇。这被称为基簇(base cluster)。

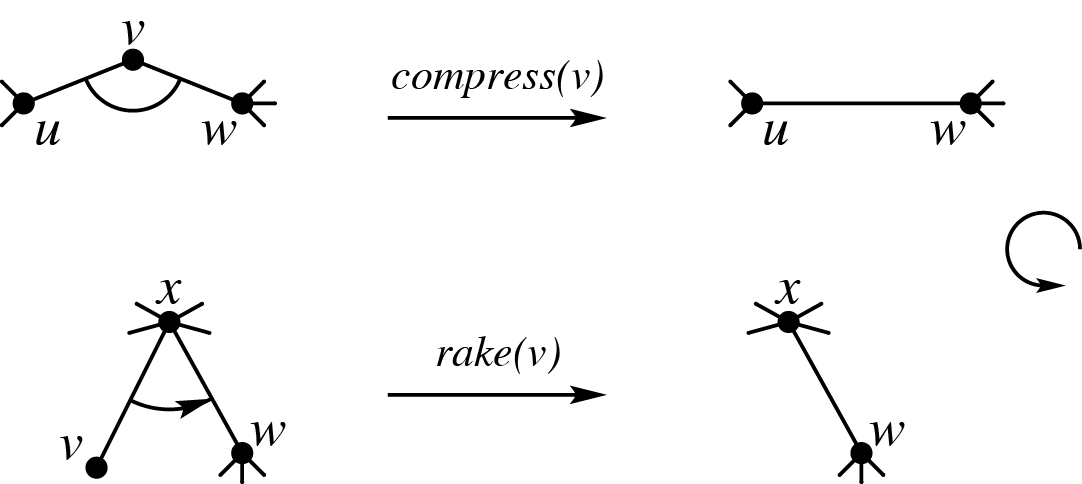
有两种对树进行的操作，Rake 和 Compress：

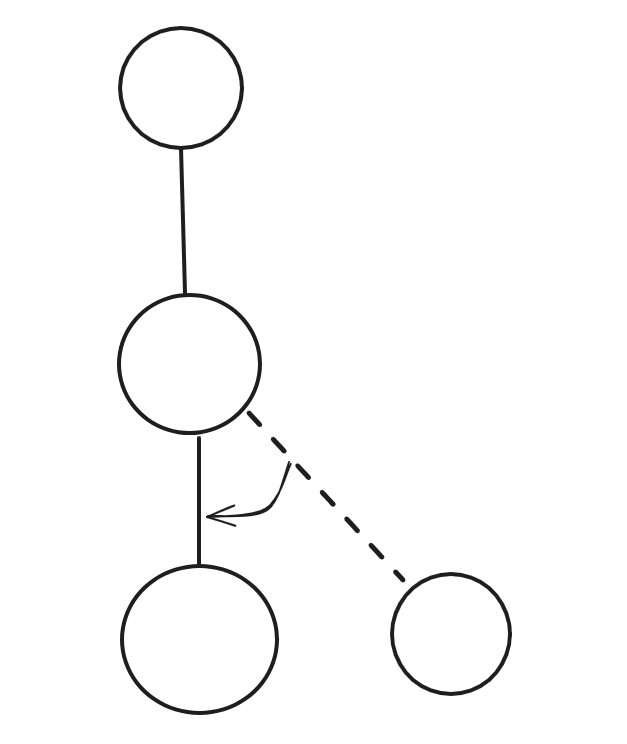
Rake 可以看作删一度点，然后把它的簇并到另一个簇上，Compress 则是缩二度点，然后合并这两个簇。

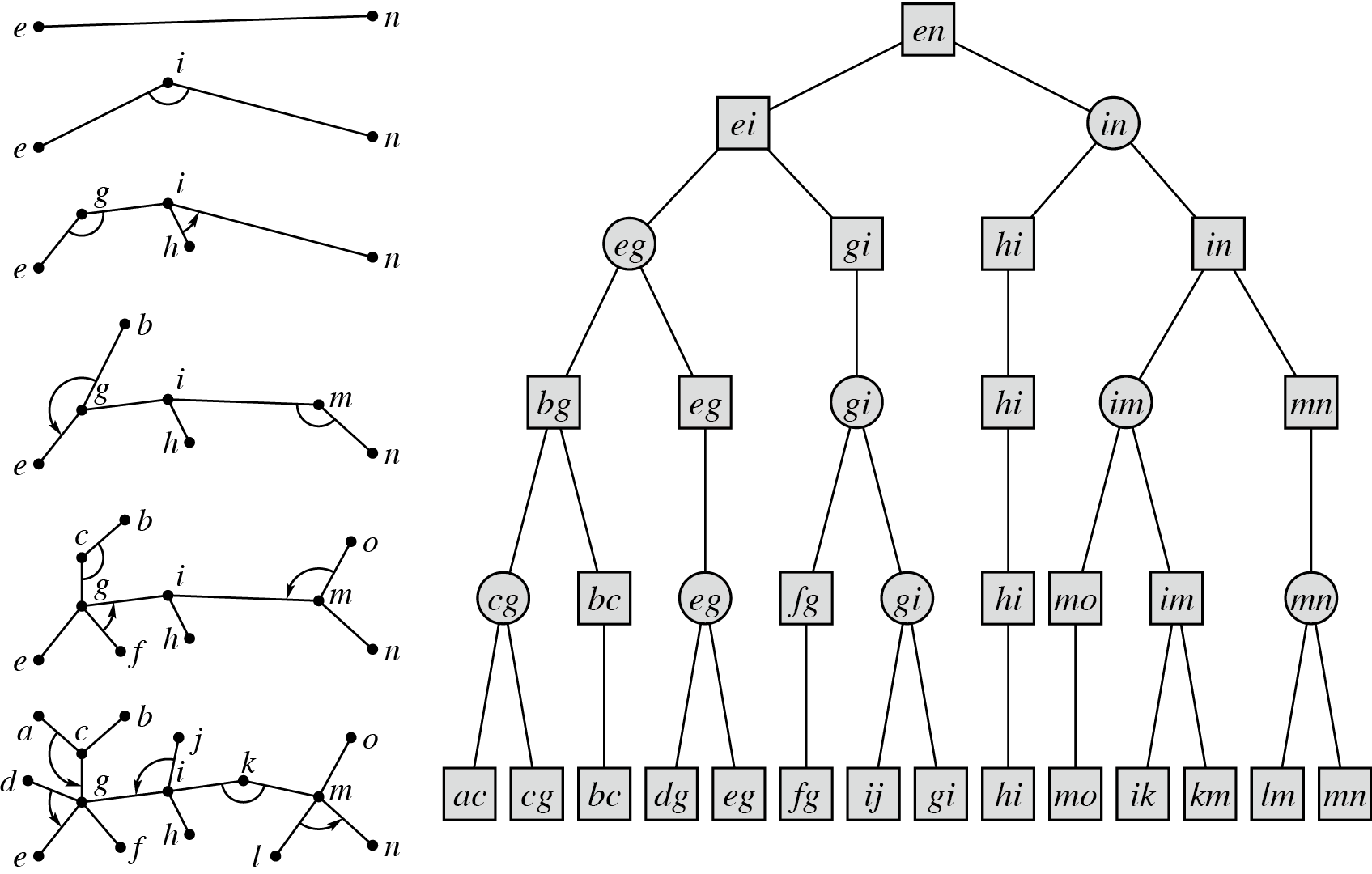
这两种操作显然都会让树的点数减小 \(1\)，并且新树的每条边都是原来的一个簇。最终，树只会剩下一条边，这条边代表的簇被称为根簇(root cluster)。

这个过程中，簇的合并结构形成了一棵树，此即 Top Tree。

通常为了维护动态信息，我们只需要维护簇路径的信息，以及簇内边集的信息，如果希望维护点集信息，需要注意的是我们不维护界点的贡献，只有界点被缩掉之后才计算其贡献。

静态 Top Tree¶

这里用的做法是基于重链剖分的那种。

考虑对每条重链，我们先把轻子树全部递归处理掉，现在的重链应当形如一条链，然后每个点再挂上若干个轻儿子。

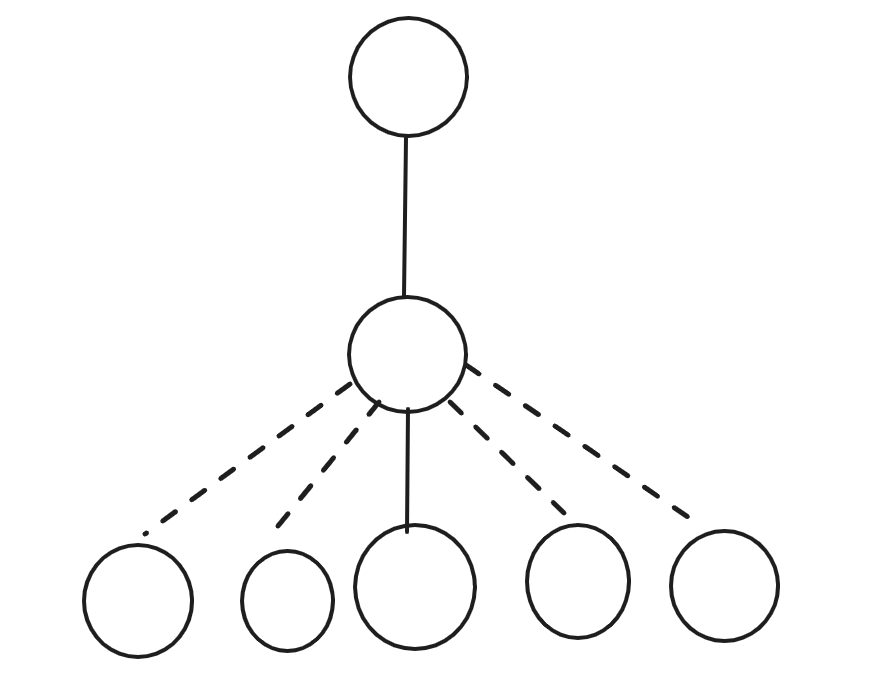
对每个点，把它轻儿子的簇排成一列，每个点的权值是它的边数，对这个序列带权分治，即每次分治分为两半，他们的权值和尽可能接近，然后把两侧得到的两个簇再 Rake 成一个簇。

现在只剩下一个簇了，再把它 Rake 到重链上。

现在整个重链只剩下一条链了，同样按边的大小带权分治 Compress 即可。

这样建出来的树有如下性质：

所有簇的界点都有祖先关系。下文中记 \(\operatorname U(x)\) 为簇 \(x\) 的上界点，\(\operatorname{D}(x)\) 为簇 \(x\) 的下界点。
簇的上界点为整个簇中深度最小的点。
Compress 树的中序遍历是按照深度升序遍历。

可以证明，树高经过两步之后必定翻倍。树高至多为 \(2\lfloor\times \log n\rfloor\)。

建树的实现¶

首先我们有 Cluster 这个类，表示一个簇的信息，其中 u 是上界点，v 是下界点。同时有 Rake 和 Compress 两个基本的操作。

首先定义 node 类

struct node {
    std::array<int, 2> ch;
    Cluster info;
    int fa, dep, type;   // type 0/1/2 分别为 base/rake/compress
    int& operator [](const int &x) {
        return ch[x];
    }
};
inline void pull(int u) {
    if (tr[u].type == 0)    return ;
    tr[u].info = (tr[u].type == 1 ? Rake : Compress)(tr[tr[u][0]].info, tr[tr[u][1]].info);
}

我们需要实现一个函数，对一个 Cluster 序列带权分治，找到其中点，将两边合并起来后再合并

inline int merge(int u, int v, int type) {
    totN++;
    tr[totN][0] = u, tr[totN][1] = v;
    tr[u].fa = totN, tr[v].fa = totN;
    tr[totN].type = type;
    pull(totN);
    return totN;
}

int Divide_And_Conquer(std::vector<int> &vec, int l, int r, int type) {
    if (l == r)
        return vec[l];
    int gsum = 0;
    for (int i = l; i <= r; i++)
        gsum += tr[vec[i]].info.siz;

    int cur = 0, mid = r - 1;

    for (int i = l; i <= r - 1; i++) {
        cur += tr[vec[i]].info.siz;
        if (cur * 2 >= gsum) {
            mid = i;
            break;
        }
    }

    int ls = Divide_And_Conquer(vec, l, mid, type);
    int rs = Divide_And_Conquer(vec, mid + 1, r, type);
    return merge(ls, rs, type);
}

最后是整棵树的建树过程：

// 到 (u, fa[u]) 的基簇的 id
int fa_id[N];
int Ssiz[N], son[N], fa[N], dep[N];
void dfs_pre(int u) {
    dep[u] = dep[fa[u]] + 1;
    Ssiz[u] = 1;
    for (const int &v : G[u]) {
        if (v == fa[u])
            continue;
        fa[v] = u;

        Cluster t = {u, v, 1};
        tr[++totN] = {{0, 0}, t, 0, 0, 0};
        fa_id[v] = totN;

        dfs_pre(v);
        Ssiz[u] += Ssiz[v];
        if (Ssiz[v] > Ssiz[son[u]])
            son[u] = v;
    }
}

int build(int tp) {
    std::vector<int> seq;
    if (fa_id[tp])
        seq.push_back(fa_id[tp]);

    for (int u = tp; son[u]; u = son[u]) {
        std::vector<int> seq2;
        // 先把轻子树全部合并起来
        for (const int &v : G[u]) {
            if (v == son[u] || v == fa[u])
                continue;
            seq2.push_back(build(v));
        }

        if (!seq2.empty()) {
            int cur = fa_id[son[u]];
            // 分治 Rake 其他子树，然后 Rake 到重儿子上
            int out = Divide_And_Conquer(seq2, 0, (int)seq2.size() - 1, 1);
            seq.push_back(merge(cur, out, 1));
        } else {
            seq.push_back(fa_id[son[u]]);
        }
    }
    return Divide_And_Conquer(seq, 0, (int)seq.size() - 1, 2);
}

全局查询¶

请注意，Top Tree 的每个簇不维护界点的贡献。

【模板】"动态DP" & 动态树分治

单点修改，树上最大权独立集。

我们知道每个簇只在界点处与外界相邻，那么令 \(f_{0/1,0/1}\) 表示两个界点分别不选/选的答案即可。

设 \(c\) 表示答案的簇，将 \(b\) \(\text{Rake}\) 到 \(a\) 上则：

\[ c_{i,j}=\max(a_{i,j}+b_{i,0},a_{i,j}+b_{i,1}+w(\operatorname{D}(b))) \]

将 \(a,b\) \(\text{Compress}\) 起来则：

\[ c_{i,j}=\max(a_{i,1}+b_{1,j}+w(\operatorname{D}(a)),a_{i,0}+b_{0,j}) \]

代码见这里，需要卡一卡常。

树链 / 子树修改与查询¶

这里主要讲维护点集信息的办法，边集信息的维护方法是几乎一样的。

树链¶

对于一个簇 \(x\)，他维护的信息是簇路径除了 \(\operatorname{U}(x)\) 的所有点信息之和，有点类似左闭右开。

设簇 \(x\) 维护的信息为 \(\operatorname{F}(x)\)，那么有：

\[ \begin{aligned} \operatorname{F}(\operatorname{Rake}(a,b))=\operatorname{F}(a)\\ \operatorname{F}(\operatorname{Compress}(a,b)) = \operatorname{F}(a)+\operatorname{F}(b); \end{aligned} \]

无论是询问还是修改一条路径 \((u, v)\) ，我们都需要找到一个簇的集合，使得他们的信息的并恰好是这条路径。

设 \(\operatorname{rson}(x)\) 是 \(x\) 在 Top Tree 上的右儿子。

考虑先找到 \((u,\operatorname{fa}(u)),(v,\operatorname{fa}(v))\) 对应的基簇在 Top Tree 上的 LCA，不妨设为 \(x\)，那么 \(\operatorname{U}(\operatorname{rson}(x))\) 一定在路径 \((u,v)\) 之间。

如果 \(x\) 是一个 \(\operatorname{Rake}\) 节点，说明 \(u,v\) 在 LCA 的两侧，这个时候 \(\operatorname{U(\operatorname{rson}(x))}\) 一定就是 \(u,v\) 的 LCA。
如果 \(x\) 是一个 \(\operatorname{Compress}\) 节点，说明 \((u,v)\) 就是一条从上到下的链，这个时候 \(\operatorname{U(\operatorname{rson}(x))}\) 就是 \((u,v)\) 之间的某个节点。

设 \(m=\operatorname{U}(\operatorname{rson}(x))\)，那么我们要处理两条直链的信息，\((\operatorname{fa}(m),u)\) 和 \((m,v)\)。这两条路径的信息同样是路径中除去最高点的所有点之和的左闭右开状物。这里的 \(\operatorname{fa}\) 是原树上的父亲，

对每个询问 \((l,r)\)，就是找到一个簇的集合，使得簇路径之并恰好为 \((l,r)\)。

考虑实现一个函数 \(\operatorname{solve}(x,l,r)\) 解决这个问题，其中 \(x\) 是一个完全包含 \((l,r)\) 的簇。

如果 \((\operatorname{D}(x),\operatorname{U}(x))\) 完全包含于 \((l,r)\)，返回 \(\operatorname{F}(x)\)。
否则，设 \(m=\operatorname{U}(\operatorname{rson}(x))\)
- 若 \(x\) 为 \(\operatorname{Compress}\) 节点
  - 如果 \(m\) 在 \((l,r)\) 之间，那么返回 \(\operatorname{solve}(\operatorname{lson}(x),l,m)+\operatorname{solve}(\operatorname{lson}(x),m,r)\)。
  - 否则，比较 \(l\) 与 \(m\) 的深浅关系。如果 \(l\) 浅于 \(m\)，那么应当返回 \(\operatorname{solve}(\operatorname{lson}(x),l,r)\)，否则是 \(\operatorname{solve}(\operatorname{lson}(x),l,r)\)。
- 若 \(x\) 为 \(\operatorname{Rake}\) 节点
  - 那么 \(\operatorname{lson}(x)\) 和 \(\operatorname{rson}(x)\) 必定有一个完全包含 \((l,r)\)，只要考虑 \(r\) 的基簇位于 Top Tree 上哪一个儿子的子树，递归那一个儿子即可。

子树¶

子树的查询就简单多了。

假设我们要查询 \(u\) 子树里所有点的信息之和，为了简便起见，我们先加上 \(u\) 这个单点的信息（\(u\) 对应的基簇），再加上所有 \(u\) 子树里除了 \(u\) 的信息之和。

仍然考虑实现一个函数 \(\operatorname{solve}(x,u)\) 表示当前簇为 \(x\)，要求出 \(u\) 子树里的所有节点信息之和，注意这里簇 \(x\) 未必包含 \(u\) 子树中的所有点。

如果这个簇为基簇或者 \(\operatorname{U}(x)=u\)，返回 \(\operatorname{F}(x)\)。
如果当前节点为 \(\operatorname{Compress}\) 节点，仍然设 \(m=\operatorname{U}(\operatorname{rson}(x))\)。
- 假设 \(m\) 深于 \(u\)（深度大于等于），返回 \(\operatorname{solve}(\operatorname{lson}(x),u)+\operatorname{F}(\operatorname{rson}(x))\)。
- 否则，返回 \(\operatorname{solve}(\operatorname{rson}(x),u)\)。
如果当前节点为 \(\operatorname{Rake}\) 节点，基簇 \((u,\operatorname{fa}(u))\) 必然在 Top Tree 上 \(x\) 的两个儿子之一，递归那一侧即可。

邻域查询¶

令 \(N_d(u)\) 表示 \(u\) 的 \(d\) 邻域。

对每个簇 \(x\)，对于上界点 \(\operatorname{U}(x)\)，我们对于每个 \(d\) 维护簇内离 \(\operatorname{U}(x)\) 距离 \(\le d\) 的点的信息之和，这里不含上界点 \(\operatorname{U}(x)\)。对于下界点 \(\operatorname{D}(x)\) 维护一样的东西，但这里是包含 \(\operatorname{D}(x)\) 的。

我们要计算 \(N_d(u)\) 里的信息之和。那么初始令簇 \(x\) 为边 \((u,\operatorname{fa}(u))\) 的基簇，假设我们已经计算出了所有簇 \(x\) 中点与 \(N_d(u)\) 的交的信息之和，现在要令 \(x\) 变为 \(x\) 在 Top Tree 上的父亲 \(y\)。

那么设 \(z\) 为 \(y\) 的 \(x\) 之外的另一个儿子，而 \(x,z\) 唯一的交点为 \(p\)，我们合并上 \(z\) 中，离 \(p\) 距离 \(\le d-\operatorname{dis}(u,p)\) 的点的信息之和即可，这可以根据我们预处理的信息维护出来。

具体的：

// tr[x].c 是 Top Tree 节点 x 代表的簇, u 为上界点, v 为下界点
// rt 为 Top Tree 的根
inline int query(int u, int d) {
    int x = fa_id[u];
    int ans = a[u];
    while (x != rt) {
        int y = tr[x].fa;
        int s = (tr[y][1] == x);
        int z = tr[y][s ^ 1];
        if (tr[y].type == 1) {
            ans += tr[z].c.Su.query(d - dis(u, tr[z].c.u));
        } else {
            if (s == 0)
                ans += tr[z].c.Su.query(d - dis(u, tr[z].c.u));
            else
                ans += tr[z].c.Sv.query(d - dis(u, tr[z].c.v));
        }
        x = y;
    }
    return ans;
}

Top Tree 邻域查询的参考实现(P6329)。

SATT¶

~~这我哪会，NOIP 没退役再说吧。~~感觉没用，不学了。