Calculating 0
心は透明 血液は酒
憧れの詩は神様みたい
本文亦可见于我的另一个博客。
FFT¶
多项式的加法,减法显然有 \(O(n)\) 的做法,而计算多项式乘法则需要 \(O(n^2)\) 的时间,我们需要一些更快的做法。
我们有一个结论:
\(n+1\) 个不同的点可以唯一确定一个 \(n\) 次多项式。
一个 \(n\) 次多项式 \(F(x)\) 就可以被写作
这被称作多项式的点值表示,而原来的表示法被称为多项式的系数表示。
证明:
假设 \(F(x)=p_0+p_1x^1+p_2x^2+\ldots + p_nx^n\)
那么我们把 \(n+1\) 个不同的 \(x\) 代入,我们可以得到一个线性方程组:
\[ \left\{\begin{aligned} F(x_0)&=p_0+p_1x_0+p_2x_0^2+\ldots+p_nx_0^n\\ F(x_1)&=p_0+p_1x_1+p_2x_1^2+\ldots+p_nx_1^n\\ F(x_2)&=p_0+p_1x_2+p_2x_2^2+\ldots+p_nx_2^n\\ &\cdots\\ F(x_n)&=p_0+p_1x_n+p_2x_n^2+\ldots+p_nx_n^n\\ \end{aligned}\right. \nonumber \]这可以被写成矩阵的形式:
\[ \begin{bmatrix} F(x_0)\\ F(x_1)\\ F(x_2)\\ \vdots\\ F(x_n)\\ \end{bmatrix} = \begin{bmatrix} 1 &x_0 &x_0^2 &\cdots &x_0^n\\ 1 &x_1 &x_1^2 &\cdots &x_1^n\\ 1 &x_2 &x_2^2 &\cdots &x_2^n\\ \vdots &\vdots &\vdots &\ddots &\vdots\\ 1 &x_n &x_n^2 &\cdots &x_n^n\\ \end{bmatrix} \begin{bmatrix} p_0\\ p_1\\ p_2\\ \vdots\\ p_n \end{bmatrix} \nonumber \]中间的是范德蒙德矩阵,由于我们选的 \(n+1\) 个 \(x\) 两两不同,则其行列式不为 \(0\),线性方程组有唯一解。
那么对于两个 \(n\) 次多项式,我们求出他们在 \(2n+1\) 个不同的 \(x\) 时的取值,然后把对应位置的值相乘,然后再还原为系数表示,我们就知道了两个多项式相乘的结果,中间相乘的过程是 \(O(n)\) 的。
唯一的问题是,我们怎么在低于 \(O(n^2)\) 的时间内求出系数表示的点值表示/把点值表示还原为系数表示?
我们最大的突破口在于可以随意选取初值,让我们尝试借助这个特性来加速求解。
为了方便,接下来我们设所要操作的多项式都是 \(2^k-1\) 次的,如果不足,可以在高次项补 \(0\)。
DFT¶
大致流程¶
一个关键的想法是,如果 \(f(x)\) 是一个偶函数,那么 \(f(x)=f(-x)\),所以我们只要计算一个点的点值就知道了两个点的点值。
如果 \(f(x)\) 是个奇函数,则 \(f(x)=-f(-x)\),仍然是计算一个值即可。
那么我们不妨把 \(F\) 分为奇偶两部分,即:
那么
再对 \(F_e(x^2)\) 与 \(F_o(x^2)\) 递归计算即可。
由于我们初始选取的所有点对都是相反数,那么递推的时候就只剩下 \(\frac{n}{2}\) 个点。如此递归计算,复杂度即为 \(O(n\log n)\)。
但是不难注意到一个问题,我们在递归子问题时,实际上代入的是 \(x^2\) 而不是 \(x\),那么我们就没有办法取相反数,因为在实数域内,\(x^2\) 总应该是正数。
让我们举一个例子看看上述过程是怎么做的,从而考察我们所选的数需要有什么性质。假设我们要将一个三次多项式 \(F(x)=-1-2x+x^2+x^3\) 转为点值表示,为此我们需要求其在四个点 \(x_0,-x_0,x_1,-x_1\) 的值,那么首先拆成:
那么,求出 \(F_e(x_0^2)\) 与 \(F_o(x_0^2)\) 的值,就可以直接推出
而 \(x_1\) 的情况类似。
接下来,我们要求 \(F_e(x)\) 在 \(x_0^2\) 与 \(x_1^2\) 处的值,并且现在 \(x_1^2=-x_0^2\),我们先不管这是怎么做到的。记 \(F_e\) 为 \(G\)。
再次类似地拆开:
因为 \(x_1^2=-x_0^2\),且我们直接知道 \(G_e(x^4)\) 与 \(G_o(x^4)\) 就是常数,所以立刻有:
并且,\(F_o\) 的情况也类似,再回退即可递推完。
总结一下,我们需要的一组 \(x\) 需要满足的性质是:
- \(x_0,x_1,x_2,\cdots,x_{2^k-1}\),其中 \(x_0,x_{2^{k-1}}\) 互为相反数,\(x_1,x_{2^{k-1}+1}\) 互为相反数……(这里的顺序与上面略有不同,为了实现方便与适配下面的内容)
- 令每个数都变为其平方,此时 \(x_0^2=x_{2^{k-1}}^2\),\(x_1^2=x_{2^{k-1}+1}^2\)……,我们去掉所有重复的数,变为 \(x_0^2,x_1^2,x_3^2,\cdots, x_{2^{k-1}-1}^2\),此时如果把他们重新标定为 \(x_0',x_1',\cdots, x_{2^{k-1}-1}'\),它们仍满足 \(1\) 中的条件,并且每次重复 \(2\) 直到序列中仅剩一个数,它们都满足 \(1\) 的条件。
实数域显然没有办法达成上述条件,考虑令 \(x\) 为复数。
单位根¶
在复数域中,一些满足我们需求的数是单位根,并且可以证明,这是唯一满足我们需求的数。
以下的 \(n\) 指的是我们所需的多项式的项数,即次数\(+1\),这意味着 \(n\) 是一个 \(2\) 的幂。
以单位圆点为起点,单位圆的 \(n\) 等分点为终点,我们可以得到 \(n\) 个复数。我们称 \(n\) 次本原单位根是它们之中幅角为正且最小的复数,也就是:
根据欧拉公式,我们将 \(\omega_n\) 写作 \(e^{i\frac{2\pi}{n}}\)(或者直接从复数乘法就是旋转的角度)可以知道:
仔细观察可以发现几条非常好的性质:
-
\(\omega_n^{k+\frac{n}{2}}=-\omega_n^k,k\in \mathbb N^+\)
这条性质我们把前面的式子展开成 \(\omega^{k}_n\omega_n^{\frac{n}{2}}\),再把后面的代入上式即可证明。
这意味着我们如果把初始的 \(x_0,x_1,x_2,\cdots, x_n\) 选为 \(\omega_n^{0},\omega_n^{1},\omega_n^{2},\cdots, \omega_n^{n-1}\)
那么这就满足上面所需的第一条要求,\(\omega_n^0\) 与 \(\omega_n^{\frac{n}{2}}\) 是一组,\(\omega_n^1\) 与 \(\omega_n^{1+\frac{n}{2}}\) 是一组……每组中均互为对方的相反数。
-
\(\omega_{kn}^{kr}=\omega_{n}^{r},r\in \mathbb N^{+}\)
这条性质仍然是直接展开即得证。
现在我们将所有数逐个平方,即变为 \(\omega_n^{0},\omega_n^{2},\omega_n^{4},\cdots, \omega^{2n-2}_n\),由于去重的原因后半部分不用管,只留 \(\omega_n^{0},\omega_{n}^2,\omega_n^{4},\cdots,\omega_{n}^{n-2}\)。
由这条性质,我们可以把上面的再写成:
\[ \omega_{\frac{n}{2}}^{0},\omega_{\frac{n}{2}}^{1},\omega_{\frac{n}{2}}^{2},\cdots,\omega_{\frac{n}{2}}^{\frac{n}{2}-1} \nonumber \]这又恰好满足了我们上面所需性质 \(2\) 中重新标定的需求!并且这一组单位根只是把 \(n\) 缩小到原来的 \(\frac{1}{2}\),自然仍然满足性质 \(1\),单位根的性质完美契合了我们的所需!
实现¶
至此我们已经可以写出将多项式的系数表示转化为点值表示的过程,只要我们将我们需要求的 \(x\) 选为 \(n\) 次单位根的各次幂即可,给出一份最朴素的实现:
//a数组最开始是系数表示
void FFT(std::complex<double> *a, int n) {
//当递归到序列长度为 1 时, n 次单位根变为原来的 n 次方, 也就是 1, 所以这个时候的值直接就是对应位置的系数
if(n == 1)
return ;
int mid = n >> 1;
//奇偶分组, 暂存下此时的系数
std::complex<double> A1[mid + 1], A2[mid + 1];
for(int i = 0; i <= n; i += 2) {
A1[i >> 1] = a[i];
A2[i >> 1] = a[i + 1];
}
FFT(A1, mid);
FFT(A2, mid);
//此时A1, A2已经是 n / 2 个点的系数表示
//wn 是 n 次单位根
std::complex<double> w0(1, 0), wn(cos(2 * pi / n), sin(2 * pi / n));
//求 x 为 w_n^0, w_n^1, w_n^1, ..., w_n^{n-1} 时分别的解
for(int i = 0; i < mid; i++, w0 *= wn) {
//F(x) = F_e(x) + x * F_o(x)
a[i] = A1[i] + w0 * A2[i];
//F(-x) = F_e(x) - x * F_o(x)
a[i + (n >> 1)] = A1[i] - w0 * A2[i];
}
}
IDFT¶
我们还得把点值表示换成系数表示,所幸这部分其实非常的简单,与 FFT 几乎完全相同。
先不管上面的 FFT 干了啥,考虑暴力的系数表示转点值表示。
这可以被写成一个线性变换的形式:
FFT 实际上就是算了上面的这样一个矩阵乘法。
所以我们只要在左边的系数表示左乘中间的范德蒙德矩阵的逆矩阵,就得到了系数表示。
中间的矩阵形式非常好,直接给出结论:其逆矩阵就是每个元素先取倒数,再除以变换长度 \(n\)。
~~为啥直接给出结论是因为我不想算了~~
而如果我们要将单位根取倒数,这实际上就是:
所以我们在 FFT 的过程中将所有单位根虚部取成相反数,所得到的就是 IDFT 的过程,至于除以 \(n\),可以在计算完成后一并解决。
//inv = 1 时为 FFT, inv = -1 时为 IDFT
void FFT(std::complex<double> *a, int n, int inv) {
if(n == 1)
return ;
int mid = n >> 1;
std::complex<double> A1[mid + 1], A2[mid + 1];
for(int i = 0; i <= n; i += 2) {
A1[i >> 1] = a[i];
A2[i >> 1] = a[i + 1];
}
FFT(A1, mid, inv);
FFT(A2, mid, inv);
//虚部乘上相反数
std::complex<double> w0(1, 0), wn(cos(2 * pi / n), inv * sin(2 * pi / n));
for(int i = 0; i < mid; i++, w0 *= wn) {
a[i] = A1[i] + w0 * A2[i];
a[i + (n >> 1)] = A1[i] - w0 * A2[i];
}
}
DFT & IDFT 的完整实现¶
完整的模板题代码是:
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <complex>
#include <cmath>
const int maxn = 1 << 22;
const double eps = 1e-6, pi = acos(-1.0);
std::complex<double> a[maxn], b[maxn];
int n, m;
void FFT(std::complex<double> *a, int n, int inv) {
if(n == 1)
return ;
int mid = n >> 1;
std::complex<double> A1[mid + 1], A2[mid + 1];
for(int i = 0; i <= n; i += 2) {
A1[i >> 1] = a[i];
A2[i >> 1] = a[i + 1];
}
FFT(A1, mid, inv);
FFT(A2, mid, inv);
std::complex<double> w0(1, 0), wn(cos(2 * pi / n), inv * sin(2 * pi / n));
for(int i = 0; i < mid; i++, w0 *= wn) {
a[i] = A1[i] + w0 * A2[i];
a[i + (n >> 1)] = A1[i] - w0 * A2[i];
}
}
int main(){
scanf("%d%d", &n, &m);
for(int i = 0; i <= n; i++) {
double x;
scanf("%lf", &x);
a[i].real(x);
}
for(int i = 0; i <= m; i++) {
double x;
scanf("%lf", &x);
b[i].real(x);
}
int len = 1 << std::max((int)ceil(log2(n+m)), 1);
FFT(a, len, 1);
FFT(b, len, 1);
for(int i = 0; i <= len; i++)
a[i] = a[i] * b[i];
FFT(a, len, -1);
for(int i = 0; i <= n + m; i++)
printf("%.0f ", a[i].real() / len + eps);
puts("");
return 0;
}
NTT¶
大量的浮点运算会带来精度误差,也会大大减缓效率,可惜在复数域 \(\mathbb C\) 中单位根是我们唯一满足需求的数,但我们大多数的多项式题中,运算实际上在 \(\mathbb Z/p\mathbb Z\) 中进行,而 \(p\) 通常是一个素数。我们希望我们所有的运算都在模意义下完成,所幸在这种情况下,FFT 有一个替代品,我们称之为 NTT,即快速数论变换。
所有复数运算都产生自单位根,如果我们希望不使用复数进行计算,就需要找到单位根的替代品。考虑我们需要单位根的哪些性质:
- \(\omega_n^{k+\frac{n}{2}}=-\omega_n^k,k\in \mathbb N^+\)
- \(\omega_{kn}^{kr}=\omega_{n}^{r},r\in \mathbb N^{+}\)
- \(\omega_n^{-1}=\cos\frac{2\pi}{n}-i\sin\frac{2\pi}{n}\)
最后一条性质是无关紧要的,我们求逆即可。
如果了解过原根的性质,我们会发现其在模 \(p\) 意义下和我们要求的东西相当接近。
不了解原根也没关系,下面简单介绍一下它在 NTT 中应用的性质:
原根与阶¶
如果正整数 \(a\) 与正整数 \(p\) 互质,并且 \(p>1\),那么对于满足 \(a^n\equiv 1\pmod p\) 的最小的 \(n\),我们称其为 \(a\) 模 \(p\) 的阶,记作 \(\delta_p(a)\)。
阶最重要的性质是,对于所有的 \(i\in [0,\delta_p(a))\),所有 \(a^i\bmod p\) 的结果两两不同。
我们反证,假设 \(k,j\in [0,\delta_p(a))\) 满足 \(a^k\equiv a^j\pmod p\),那么 \(a^{k-j}\equiv 1\pmod p\),与定义矛盾。
而如果 \(g\) 与 \(n\) 满足 \(\delta_n(g)=\varphi(n)\),且 \(\gcd(g,n)=1\),则 \(g\) 为 \(n\) 的一个原根。
如果 \(\gcd(g,n)=1\) 且 \(n>0\),那么 \(g\) 为 \(n\) 的一个充要条件是 \(\{g^1,g^2,g^3,\cdots, g^{\varphi(n)}\}\) 是 \(n\) 的一组简化剩余系。这是因为由阶的定义,集合中的任意两个元素模 \(n\) 不同余,且 \(\gcd(g,n)=1\),则该集合就是 \(n\) 的一组简化剩余系。
说了这么多定义,原根到底为什么满足我们上面的要求?
通常模数都是素数,那么 \(\varphi(p)=p-1\),所以 \(p\) 的一个原根 \(g\) 自然满足 \(\gcd(p,n)=1\),则 \(g\) 的从 \(1\) 到 \(p-1\) 次方在模 \(p\) 意义下可以取遍 \(1\sim p-1\) 中的每一个值。并且每个值唯一对应一个 \(g^k,k\in[1,p-1)\)
现在我们假设 \(n | (p-1)\),\(n\) 与上面意义相同,都是 \(2\) 的某个幂,定义
根据费马小定理,我们有 \(g_n^n=g^{n\frac{p-1}{n}}=g^{p-1}=1\),也就是这仍然是每 \(n\) 次方一循环的,与单位根相同。
单位根的性质 \(1\),\(\omega_n^{k+\frac{n}{2}}=-\omega_n^k,k\in \mathbb N^+\) 可以被等价地叙述为 \(\omega_n^{\frac{n}{2}}=-\omega_n\)
让我们考虑 \(g_n^{\frac{n}{2}}\):
又因为
根据原根的定义,\(g^{\frac{p-1}{2}}\) 必定不与 \(1\) 同余,因为如果这样就不满足每一个值唯一对应一个 \(g^k,k\in[1,p-1)\)
所以就一定有:
满足我们所需的性质 \(1\)。
对于满足性质 \(2\) 的证明是简单的:
所以如果我们直接把上面 FFT 的代码中的单位根全部替换成对应的 \(g_n\),就可以得到 NTT 的代码了。
唯一的问题是,我们总是需要满足 \(n|p-1\),而我们常用的模数 \(998244353\) 满足 \(998244352=7\times17\times2^{23}\),而 \(1004535809\) 满足 \(1004535808=479\times 2^{21}\),\(469762049\) 满足 \(469762048=7\times 2^{26}\),可惜的是 \(1000000007\) 的性质就要差得多,\(1000000006=2\times 500000003\),对于这种情况,我们将在后面介绍解决方法。
到这里我们就可以写出 NTT 了,但这个多项式乘法也太慢了,能不能更猛一点啊?
优化¶
位逆序置换 / 蝴蝶变换¶
上面的实现中,我们每次递归都要申请两个长度为 \(mid\) 空间,做一遍分拆系数……
最大的问题在于我们要分拆系数赋值,如果我们从一开始就把每个系数放到目标位置上,那么我们就直接两个两个合并,四个四个合并……每次倍增即可完成整个过程。
考虑我们是怎么把每个系数 \(a_i\) 放到目标位置上的。
从低到高逐位考虑 \(i\) 二进制的每一位,如果是 \(1\) 我们就把他放在序列右半边,递归右边,如果是 \(0\) 就放到序列左半边,递归左半边。
不难想到这样逐步进行下去,递归到底时其位置就是 \(i\) 的二进制翻转
那么我们直接把每个系数要放到的位置处理出来,然后两两合并就可以了,省去了中间大量的申请内存与复制的时间。
而目标要换到的位置实际上是可以线性预处理出来的,假设 \(\operatorname{rev}(i)\) 表示下标为 \(i\) 的系数最终要移动到的位置。
从小到大做,而 \(\operatorname{rev}(0)=0\)
那么我们已经知道了 \(\operatorname{rev}(\lfloor\frac{i}{2}\rfloor)\) 的结果。我们要翻转 \(i\),可以看做先翻转 \(\lfloor\frac{i}{2}\rfloor\),将其右移一位,然后再最高位上填上末尾。
举个例子,我们要翻转 \(\color{red}{01101010}\color{green}1\),我们已经知道了 \(0\color{red}01101010\)(先去掉末位再在前面补 \(0\)),那么翻转之后就是 \(\color{red}{01010110}\color{black}{0}\),去掉最后一位变成 \(\color{red}{01010110}\),随后在最前面补上 \(1\),就变成 \(\color{green}1\color{red}{01101010}\),这就是我们所需的翻转。
假设整个序列的长度是 \(2^k\),那么:
接下来考虑怎么合并答案。
现在假设我们已经有了 \(F_e(\omega_{n/2}^{k})\) 和 \(F_o(\omega^{k}_{n/2})\) 的答案,那么他们分别存在数组里 \(k\) 与 \(k+\frac{n}{2}\) 的位置,而我们借助这两个值算出来的 \(F(\omega_n^{k})\) 与 \(F(\omega^{k+\frac{n}{2}}_n)\) 恰好放在同样的位置,直接覆盖即可。
具体实现可以看代码:
int k = std::max((int)ceil(log2(n+m)), 1);
int len = 1 << k;
//预处理rev
for(int i = 0; i < len; i++)
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (k - 1));
void NTT(ll *a, int n, int inv){
//将系数换到置换对应的位置
for(int i = 0; i < n; i++)
if(i < rev[i])
std::swap(a[i], a[rev[i]]);
//变换的区间长度
for(int i = 1; i < n; i <<= 1) {
//这部分可以预处理单位根做到更快
ll gn = f_pow(inv ? g : gi, (mod - 1) / (i << 1));
for(int j = 0; j < n; j += (i << 1)) {
ll g0 = 1;
for(int k = 0; k < i; k++, g0 = g0 * gn % mod) {
//直接覆盖原来的值
ll x = a[j + k], y = g0 * a[i + j + k] % mod;
a[j + k] = (x + y) % mod;
a[i + j + k] = (x - y + mod) % mod;
}
}
}
}
这还可以通过减少取模次数进一步优化。
能不能再猛一点啊?¶
上面的 NTT 再加上预处理单位根与逆元就已经足够应付大多数的情况,下面的内容可以暂时略过。
参考资料:
yhx-12243 的 NTT 到底写了些什么(详细揭秘) - Seniorious' blog
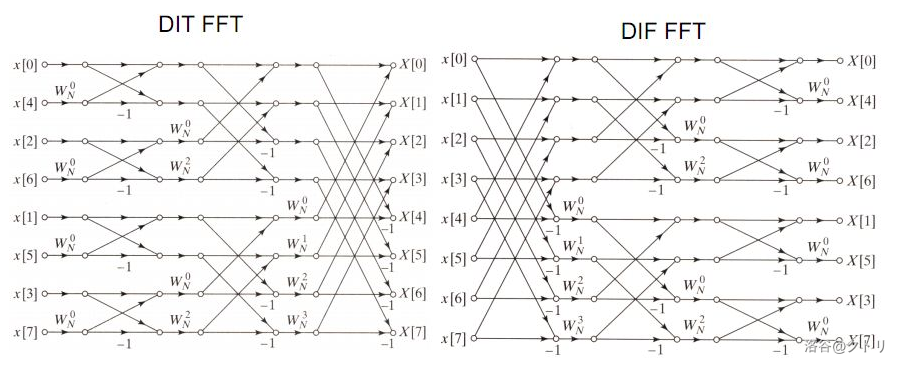
DIF-FFT¶
上面的每次按奇偶划分的做法被称为DIT(按时域抽取)-FFT,其作用可以概括为输入一个经过蝴蝶变换后的系数向量,输出一个点值向量
而DIF(按频域抽取)-FFT是其转置,作用是输入一个系数向量,输出一个蝴蝶变换后的点值向量
太抽象了,先不管这玩意是啥意思,我们考虑换一个角度做 FFT,现在我们已经知道 FFT 的取值都是单位根了,我们从单位根下手:
假设我们要求 \(F(\omega_n^k)\)
按 \(k\) 的奇偶性分类讨论,如果我们的 \(k\) 是一个偶数,那么
如果我们的 \(k\) 是一个奇数,那
这样似乎还是要对每个点求一次单位根,是 \(\mathcal O(n^2)\) 的,但是不要忘记单位根的性质
对于所有偶数的 \(k\),都写成 \(\omega_{n}^{2p}\) 的形式,也就是 \(\omega_{n/2}^{p}\),这也就是说,我们把奇数的位置全部乘上 \(\omega^{1}_{n}\),再把奇数和偶数的部分提取出来,分别递归进行 DIF,那么在第二层乘上 \(\omega^{1}_{n/2}\) 实际上就是在第一层乘上了 \(\omega^{2}_n\)。考虑幂次上的二进制拆分,所以这个是对的。
这里的做法其实是考虑每一个系数会乘上哪些单位根,而 DIT-FFT 实际上是考虑每一个单位根会乘上哪些系数。
最后实际上把所有 \(F(\omega_n^{k})\) 按 \(k\) 蝴蝶变换了一遍,所以就是输入一个系数向量,输出一个蝴蝶变换后的点值向量
我们有一份非常暴力的实现:
std::vector<std::complex<double>> dif_fft(std::vector<std::complex<double>>& x) {
int N = x.size();
if (N == 1) {
return x;
}
std::vector<std::complex<double>> even(N / 2);
std::vector<std::complex<double>> odd(N / 2);
for (int i = 0; i < N / 2; i++) {
even[i] = x[i] + x[i + N / 2];
odd[i] = (x[i] - x[i + N / 2]) * std::polar(1.0, -2 * M_PI * i / N);
}
std::vector<std::complex<double>> evenResult = dif_fft(even);
std::vector<std::complex<double>> oddResult = dif_fft(odd);
std::vector<std::complex<double>> result(N);
for (int k = 0; k < N / 2; k++) {
result[k] = evenResult[k];
result[k + N / 2] = oddResult[k];
}
return result;
}
巧的是,我们原本的 DIT-FFT 是输入一个经过蝴蝶变换后的系数向量,输出一个点值向量,而 DIF-FFT 是输入一个系数向量,输出一个蝴蝶变换后的点值向量。
那我们直接先 DIF-FFT 得到蝴蝶变换后的点值向量,再 DIT-FFT 翻转回来不就能得到系数向量了吗?
直接按这样实现可以再卡大概 \(70\text{ms}\)。
再优化¶
DIT-FFT因为从小到大,每层都要重新处理单位根,单位根乘法是 \(O(n\log n)\) 次的。
DIF-FFT因为从大到小,但是每层计算的时候都要即时贡献,单位根乘法也是 \(O(n\log n)\) 次的。
那如果我们直接对不蝴蝶变换的系数向量做 DIT-FFT 呢?
我们仍然会得到一个点值的数组,而其正是蝴蝶变换后的数组,只要我们对中途用到的原根也蝴蝶变换一下就行了。
更具体的,我们可以在 DIF-FFT 的过程中做 DIT-FFT,也就是说,我们除了最外层大循环以外都是 DIT-FFT 的操作,对 DIT-FFT 也可以像这样直接反过来。这样我们的原根移动次数可以优化到 \(O(n)\) 级别的。
对于预处理原根的方法,我们也可以改变一下,以 \(\bmod 998244353\) 举例,我们考虑每次用到的原根都是 \(3^{\frac{p-1}{n}}\),而 \(n\) 是 \(2\) 的幂,把 \(p\) 拆成 \(7\times 17\times 2^{23}=119\times 2^{23}\) 的形式,我们把原来的底数从 \(3\) 换成 \(3^{119}\),这样我们只要维护底数的各个幂即可。
至于如何直接预处理蝴蝶变换后的原根,先直接预处理出 \(g^{2^k}\) 放在 \(2^{21-k}\) 处,也就是蝴蝶变换后的结果,为什么是 \(21-k\) 次方是因为 \(\frac{p-1}{n}\) 对应的就是它。
其次 \(g^{2^j+2^k}=g^{2^j}\times g^{2^k}\),每次拿两个位拼起来就行了
#include <algorithm>
#include <vector>
#include <cctype>
#include <cmath>
#include <cstring>
#include <iostream>
typedef long long ll;
using namespace std;
const ll g = 3, gi = 332748118, mod = 998244353;
// 3^119
const ll prebase = 15311432;
const int N = 2e6 + 1e5 + 10;
ll f_pow(ll a, ll k) {
ll base = 1;
for (; k; k >>= 1, a = a * a % mod)
if (k & 1)
base = base * a % mod;
return base;
}
namespace NTT {
ll w2[N];
int n;
void init(int n = N) {
int t = min((n > 1 ? __lg(n) - 1 : 0), 21);
// 直接预处理蝴蝶变换后的单位根
w2[0] = 1, w2[1 << t] = f_pow(prebase, 1 << (21 - t));
// 翻转后的单位根, 大的对应小的
for (int i = t; i; i--)
w2[1 << (i - 1)] = w2[1 << i] * w2[1 << i] % mod;
// 除去最后一个 1 与只留最后一个 1, 这个时候本身就是已经倒序的, 自然这样处理出来的也是倒序的
for (int i = 1; i < (1 << t); i++)
w2[i] = w2[i & (i - 1)] * w2[i & -i] % mod;
}
inline void NTT_init(int len) {
n = 1 << len;
}
void DIF(vector<ll> &a) {
// 外层循环是 DIT
for (int i = n >> 1; i >= 1; i >>= 1) {
for (int j = 0, og = 0; j < n; j += (i << 1), og++) {
for (int k = 0; k < i; k++) {
ll x = a[j + k], y = a[i + j + k] * w2[og] % mod;
a[i + j + k] = (x - y + mod) % mod;
a[j + k] = (x + y) % mod;
}
}
}
}
void DIT(vector<ll> &a) {
// 外层循环是 DIF
for (int i = 1; i < n; i <<= 1) {
for (int j = 0, og = 0; j < n; j += (i << 1), og++)
for (int k = 0; k < i; k++) {
ll y = (a[j + k] + a[i + j + k]) % mod;
a[i + j + k] = (a[j + k] - a[i + j + k] + mod) * w2[og] % mod;
a[j + k] = y;
}
}
}
inline void DNTT(vector<ll> &a) {
DIF(a);
}
inline void IDNTT(vector<ll> &a) {
DIT(a);
reverse(a.begin() + 1, a.begin() + n);
ll inv = f_pow(n, mod - 2);
for (int i = 0; i < n; i++)
a[i] = a[i] * inv % mod;
}
}
int n, m;
vector<ll> a, b;
int main() {
scanf("%d%d", &n, &m);
a.resize(n + m + 1, 0);
b.resize(n + m + 1, 0);
for (int i = 0; i <= n; i++)
scanf("%lld", &a[i]);
for (int i = 0; i <= m; i++)
scanf("%lld", &b[i]);
int k = std::max((int)ceil(log2(n + m + 1)), 1);
NTT::init();
NTT::NTT_init(k);
a.resize(1 << k);
b.resize(1 << k);
fill(a.begin() + n + 1, a.begin() + (1 << k), 0);
fill(b.begin() + m + 1, b.begin() + (1 << k), 0);
NTT::DNTT(a);
NTT::DNTT(b);
for (int i = 0; i < (1 << k); i++)
a[i] = a[i] * b[i] % mod;
NTT::IDNTT(a);
for (int i = 0; i < n + m + 1; i++)
printf("%lld ", a[i]);
puts("");
return 0;
}
听说还能再快点 最新最热多项式乘法常数优化 - Kevin090228 的博客 但是摆了。